数学初三上 第二十六章 二次函数
26.2 特殊二次函数的图像 第三课时（1）
1、选择题
1. 关于
和
的图像的说法：①它们都是轴对称图形；②它们的顶点相同，对称轴也相同；③它们都是抛物线；④两个函数图像关于x轴对称。这类说法正确的有 （ ）
A． 4个 B. 3个 C. 2个 D. 1个
2. 关于二次函数
，下列说法正确的是 （ ）
A．若a>0，则y随x的增大而增大 B. 若a>0，则y随x的增大而减小
C. 若a<0，则y有最小值 D. 若a>0，则y有最小值
3.关于二次函数
与
的图像，下列结论不正确的是（ ）
A．它们都是抛物线 B. 它们都是轴对称图形
C. 这两个函数图像具备相同的对称轴 D. 两个函数图像关于y轴对称
4. 已知点（m-1，y1）、（m，y2）、（m+1，y3）均在函数
的图像上，则y1、y2、y3的大小关系是 （ ）
A．y1>y2=y3 B. y2> y1 =y3 C. y1=y2=y3 D. y2< y1=y3
5. 在同一坐标系内二次函数与一次函数
的图像大致是 （ ）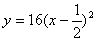
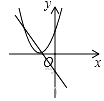
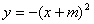
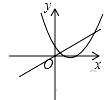
A． B. C. D.
6. 二次函数
的图像向左平移2个单位长度，得到新的图像的二次函数表达式是 （ ）
A．
B. 
C. 
D. 
2、填空题
7．若抛物线
经过点（0，-8），则a=__________，这个抛物线的分析式为__________。
8. 抛物线
向左平移个单位长度得到的抛物线的分析式是 _________________.
9. 若点A（2，-4）在函数的图像上，则m=__________，这条抛物线的对称轴是直线__________，点A关于抛物线对称轴的对称点的坐标是__________。
10. 抛物线的图像向__________平移 __________个单位长度得到抛物线
。
11. 抛物线
可以看作由抛物线
向__________平移__________个单位得到的。
12. 将抛物线向右平移5个单位得到的抛物线的函数分析式是__________。
13. 抛物线y=-22的对称轴是_________________，顶点坐标是_________________，图象开口向_________________.
14. 抛物线先向左平移2个单位长度，再向上平移5个单位长度，得到的抛物线的表达式为__________。
15. 在下表空格处填入有关的内容：
二次函数 | |||||||
图像 | 对称性 | 开口方向 | 开口大小 | 顶点坐标 | y随x的变化状况 | ||
|
| a>0 | a<0 |
|
| a>0 | a<0 |
|
|
|
| ||||
3、解答卷
16. 已知函数
与
。
（1）完成下表：
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（2）打造平面直角坐标系，并在坐标系中作出二次函数与的图像；
（3）抛物线与之间有哪些关系？它们是轴对称图形吗？它们的对称轴和顶点坐标分别是什么？
（4）随x的增大，y分别是怎么样变化的？
17. 假如把抛物线向下平移2个单位，再向左平移4个单位长度后得到抛物线，试求a,b的值。
18、若抛物线
向上平移3个单位长度后经过点（2，7），求平移后的抛物线的分析式。
19. 已知抛物线经过点（-1，3），且抛物线的顶点坐标为（-2，0），求此抛物线的函数分析式。
20. 已知抛物线经过点（1，4），且关于直线
对称，求这个二次函数的分析式。
21. 已知二次函数
的形状和
相同，且顶点坐标为（-3，0），求抛物线关于y轴对称的图形的函数分析式。
22. .求抛物线向右平移3个单位长度后得到的分析式。
数学初三上 第二十六章 二次函数
26.2 特殊二次函数的图像 第三课时（1）
参考答案
1.A 2. D 3. C 4. D 5. C 6. B
7. a=-2
8. 
9. 0或-4 x=0或x=4 或（6，-4）
10. 左 3
11. 左 2
12. 
13. 直线x=1 向下
14. 
15.
二次函数 | |||||||
图像 | 对称性 | 开口方向 | 开口大小 | 顶点坐标 | y随x的变化状况 | ||
抛物线 | 关于直线x=-m对称 | a>0 | a<0 | |a|越大，开口越小；|a|越小，开口越大 | （-m,0） | a>0 | a<0 |
向上 | 向下 | 当 | 当 | ||||
16. （1）略 （2）略
（3）抛物线和都可看作是由
平移得到的，即它们的开口方向相同，开口的大小相同，形状相同，它们是轴对称图形，它们的对称轴分别是直线，顶点的坐标分别是（1，0），（-1，0）
（4）二次函数：当
时，y随x的增大而减小，当
时，y随x的增大而增大；二次函数：当时，y随x的增大而减小，当
时，y随x的增大而增大
17. 
18. 
19. 
20.
21.
22.
