上大附中2018-2019学年第一学期高中三年级首次月考数学试题
注意:本试题共有21道考试试题,满分150分,考试时间120分钟,答案做在答卷纸上。
1、填空题
1.行列式![]()
![]() ___________.
___________.
2.双曲线![]() 的渐近线方程是__________.
的渐近线方程是__________.
3.不等式![]() 的解集是________.
的解集是________.
4.若![]() 满足
满足![]() ,则
,则![]() 的最小值是_________.
的最小值是_________.
5.掷一颗均匀的骰子,则点数大于1且不大于5的概率是_________.
6.设,则![]() ________.
________.
7.已知![]() ,且
,且![]() ,则
,则![]() 的最小值为________.
的最小值为________.
8.在△ABC中,设三个内角A、B、C所对的边分别为![]() ,且
,且![]() 则△ABC的面积为__________.
则△ABC的面积为__________.
9.若函数![]() 有反函数,则
有反函数,则![]() 的取值范围是________.
的取值范围是________.
10.若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不一样的实数解,则
上有两个不一样的实数解,则![]() 的取值范围为________.
的取值范围为________.
11.已知![]() 函数
函数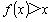 若对任意
若对任意![]() 恒成立,则
恒成立,则![]() 的取值范围是______.
的取值范围是______.
12.如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=2,若点E为边CD上的动点,则![]() 的最小值为________.
的最小值为________.
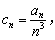
2、选择题
13.设![]() 则“
则“![]() ”是“
”是“![]() ”的
”的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也非必要条件
14.数列![]() 中,
中,![]() ,且
,且![]() ,则目前
,则目前![]() 项和
项和![]() 最小时,
最小时,![]() 的值是
的值是
A.6 B.7 C.8 D.9
15.若![]() 为奇函数,且实数
为奇函数,且实数![]() 满足
满足![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.以上答案都不对
D.以上答案都不对
16.已知当![]() 时,有
时,有![]() 依据以上信息,若对任意
依据以上信息,若对任意
![]() ,都有
,都有![]() 则
则![]()
A.-444 B.-455 C.-466 D.以上答案都不对
3、解答卷
17.
如图,直三棱柱![]() 的底面为直角三角形,两直角边AB和AC的长分别为4和3,侧棱
的底面为直角三角形,两直角边AB和AC的长分别为4和3,侧棱![]() 的长为5.
的长为5.
求直三棱柱![]() 的侧面积;
的侧面积;
若M为棱![]() 上的中点,求直线AM与平面
上的中点,求直线AM与平面![]() 所成角的大小.
所成角的大小.

18.
已知![]()
当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
若![]() 时不等式
时不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
19.
已知数列![]() 满足
满足![]() 设
设![]()
求数列![]() 的通项公式;
的通项公式;
![]() 求数列
求数列![]() 的最小值。
的最小值。
20.
设椭圆![]() 的左焦点为F,过F的直线
的左焦点为F,过F的直线![]() 与C交于A、B两点,点M的坐标为.
与C交于A、B两点,点M的坐标为.
若点F也是顶点为原点的抛物线![]() 的焦点,求抛物线
的焦点,求抛物线![]() 的方程;
的方程;
当![]() 与
与![]() 轴垂直时,求直线AM的方程;
轴垂直时,求直线AM的方程;
设O为坐标原点,证明:∠OMA=∠OMB.
21.
对于概念域为![]() 的函数
的函数![]() ,假如同时满足以下三个条件:
,假如同时满足以下三个条件:
①任意的![]() ,总有f
,总有f![]() ;
;
②![]()
③若![]() 总有
总有![]() 成立.
成立.
则称函数![]() 为理想函数.
为理想函数.
证明:若函数![]() 为理想函数,则
为理想函数,则![]()
证明:函数![]() 是理想函数;
是理想函数;
证明:若函数![]() 为理想函数,假定存在
为理想函数,假定存在![]() 使得
使得![]() 且
且![]() 则
则
![]()







