《3.2 一元一次方程的应用》基础训练
1. 书店里每本定价10元的书,本钱是8元.为了营销,书店决定让利10%给读者,问该书应优惠.
A. 9.7 B. 9.6 C. 9.8 D. 9.5
2. 某商场节日酬宾:全场8折.一种电器在这次酬宾活动中的价值率为10%,它的进价为2000元,那样它的原价为.
A. 2750元 B. 2650元 C. 2850元 D. 2950元
3. 李师傅用100000元存了一个一年期的按期储蓄,到期后本息和共102250元,则这种储蓄的年利率是.
A.1.25% B.2.5% C. 2.25% D.2.75%
4. 五一期间,某电器按本钱价提升30%后标价,再打8折销售,价格为2080元,设该电器的本钱价为x元,依据题意,下面所列方程正确的是.
A.x×80%=2080 B.x·30%·80%=2080
C.2080×30%×80%=x D.x·30%=2080×80%
5. 某次成语英雄赛中有25道题,答对一题记5分,答错或不答一题扣2分,比赛结束后小明共得到90分,试问小明答对了道题.
A.30 B.25 C.35 D.20
6. 某厂第一车间有64人,第二车间有56人.现因工作需要,需要第一车间人数是第二车间人数的一半.需从第一车间调人到第二车间.
A.22 B.23 C.24 D. 25
7. 一个长方形的周长为30 cm,若这个长方形的长降低1 cm,宽增加2 cm就可成为一个正方形,设长方形的长为x cm,可列方程为.
A.x+1=-2 B.x+1=-2
C.x-1=+2 D.x-1=+2
8. 一个三角形的三条边的长度之比为2∶4∶5,最长的边比最短的边长6 cm,则该三角形的周长是.
A.22 B.24 C.26 D.28
9. 将装满水的底面直径为40厘米,高为60厘米的圆柱形水桶里的水全部灌于另一个底面直径为50厘米的圆柱形水桶里,这个时候水面的高度是.
A. 38厘米 B. 38.1厘米 C. 38.3厘米 D. 38.4厘米
10. 有一个长、宽、高分别是15 cm、10 cm、30 cm的长方体钢锭,现将它锻压成一个底面为正方形,且边长为15 cm的长方体钢锭,则锻压后长方体钢锭的高为.
A.10cm. B.20cm. C.15cm. D.25cm.
11. 将一个长、宽、高分别为15cm、12cm和8cm的长方体钢坯锻导致一个底面是边长为12cm的正方形的长方体钢坯.试问:是锻造前的长方体钢坯的表面积大,还是锻造后的长方体钢坯的表面积大?请你计算比较.
12. 小明家离学校2.9千米,一天小明放学走了5分钟之后,他父亲开始从家出发骑自行车去接小明,已知小明每分钟走60米,父亲骑自行车每分钟骑200米,请问小明父亲从家出发几分钟后接到小明?
13. 敌我两军相距25km,敌军以5km/h的速度逃跑,我军同时以8km/h的速度追击,并在相距1km处发生战斗,问战斗是在开始追击后几小时发生的?
14. 张师傅在银行里用按期一年整存整取的方法存入人民币8000元,到期得到本息8180元,求这项储蓄的月利率.
15. 一件夹克按本钱价提升50%后标价,后因季节关系按标价的8折供应,每件以60元卖出,这批夹克每件的本钱价是多少元?
答案和分析
【答案】
1. C 2. A 3. C 4. A 5. D
6. C 7. D 8. A 9. D 10. B
11. 锻造前的长方体钢坯的表面积较大.
12. 小明父亲从家出发 10分钟后接到小明.
13. 战斗是在开始追击后8小时发生的.
14. 这项储蓄的月利率为0.1875%.
15. 这批夹克每件的本钱价是50元.
【分析】
1. 解:设该书应打x折,
依据题意,得10×![]() -8=×.
-8=×.
解得,x=9.8.
答:该书应打九八折.
故选C.
本题中的价值为10-8=2,由于让利10%给读者,所以书店的价值为×2,此时的价格为元.依据产品收益=产品价格-产品进价,就能打造起方程.
让利10%,即指收益为原来的90%.解题时应该注意理解题目内包括的信息.
2. 解:设原价为x元,
依据题意,得80%x-2000=2000×10%.
解得,x=2750.
答:它的原价为2750元.
故选A.
本题中的价值为元,销价格为元,依据公式打造起方程即可.
价格=进价+收益,价格=原价×优惠数×0.1,价格=进价×.
3. 解:设这种储蓄的年利率是x,
依据题意,得100000×=102250,
解得,x=2.25%.
答:这种储蓄的年利率是2.25%.
故选C.
本题中的本息和共102250元,本金是100000元,依据公式打造起方程即可.
利息=本金×年利率×年数;本息和=本金+利息.
4. 解:设该电器的本钱价为x元,那样提升本钱价后该电器的标价为x,对它打8折得实质价格为x×80%.
依据题意,得x×80%=2080.
故选A.
产品的价值是产品的价格与进价之差,也就是说:收益=实质价格-进价.产品利率是:利率=产品收益产品进价×100%.打8折后的价格为原价的80%.
5. 解:设小明答对了x道题,则答错或不答 道题,
依据题意,得5x-2=90,
解得,x=20.
答:小明答对了20道题.
故选D.
由“成语英雄赛中有25道题”,设小明答对了x道题,则答错或不答 道题,依据答对的题数×5-答错或不答的题数×2=最后得分数,就能打造起方程.
本题解题的重点在于依据已知条件确定两者的数目关系,然后列出方程解题.
6. 解:设需从第一车间调x人到第二车间,
依据题意得2=56+x,
解得,x=24.
答:需从第一车间调24人到第二车间.
故选C.
本题中设需从第一车间调x人到第二车间,则调配完之后,第一车间有人,第二车间有人.依据“第一车间人数是第二车间人数的一半”,就能打造起方程.
本题解题的重点在于依据已知条件确定两者的数目关系,然后列出方程解题.
7. 解:由于长方形的长为x cm,长方形的周长为30 cm,所以长方形的宽为cm.
由于这个长方形的长降低1 cm,宽增加2 cm就可成为一个正方形,
所以x-1=+2.
故选D.
依据长方形的周长公式,表示出长方形的宽,再由正方形的四条边都相等得出等式即可.
8. 解:设该三角形的边长分别为2x cm,4x cm,5x cm.
由题意得,5x-2x=6,
解得,x=2.
所以2x+4x+5x=11x=11×2=22,
即该三角形的周长为22 cm.
故选A.
借助三角形最长的边比最短的边长6 cm为相等关系列出方程.设其中一份为x cm,由三角形的三条边的长度之比,即可用含x的式子表示出来.
比率分配问题中的全部数目=各种成分的数目值之和.
9. 解:设这个时候水面的高度为x厘米,
依据题意可得:![]() ,
,
解得,x=38.4.
答:这个时候水面的高度为38.4厘米.
故选D.
本题中的相等关系为:底面直径为40厘米,高为60厘米的圆柱形水桶中水的体积=底面直径为50厘米的圆柱形水桶中水的体积,故可设这个时候水面的高度为x厘米,用含x的式子表示出水的体积即可.
10. 解:设锻压后长方体钢锭的高为x cm.
由题意,得 15×15×x=15×10×30,
解得,x=20 .
答:锻压后长方体钢锭的高为20cm.
故选B.
由锻压前后两长方体钢锭体积相等,可求出锻压后长方体钢锭的高.
本题的解题重点是依据等积变形中的等量关系确定变化后长方体的高.
11. 解:设锻造后长方体的高为xcm,
依题意,得15×12×8=12×12x.
解得,x=10.
锻造前长方体钢坯的表面积为
2×=2×=792,
锻造后长方体钢坯的表面积为
2×=2×=768.
由于792>768,所以锻造前的长方体钢坯的表面积较大.
由锻造前后两长方体钢坯体积相等,可求出锻造后长方体钢坯的高.再计算锻造前后两长方体钢坯的表面积,最后比较大小即可.
本题的解题重点是依据等积变形中的等量关系确定变化后长方体的高.
12. 解:设小明父亲出发x分钟后接到小明,如图所示,
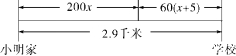
由题意,得200x+60=2900.
解得x=10.
答:小明父亲从家出发 10分钟后接到小明.
本题等量关系:小明所走的路程+父亲所走的路程=全部路程,但应该注意小明比父亲多走了5分钟,另外也应该注意本题单位的统一.
找出问题中的等量关系是列方程解应用题的重点,对于行程问题,一般借用“线段图”来剖析问题中的数目关系.如此可以比较直观地反映出方程中的等量关系.
13. 解:设战斗是在开始追击后x小时发生的.
依据题意,得8x-5x=25-1.
解得,x=8.
答:战斗是在开始追击后8小时发生的.
本题相等关系:我军所走的路程-敌军所走的路程=敌我两军相距的路程.
追及问题中的等量关系:追及距离=速度差×追准时间.
14. 解:设这项储蓄的月利率为x,
依据题意,得8000+8000×12×x=8180.
解方程得,x=0.1875%.
答:这项储蓄的月利率为0.1875%.
本题考查储蓄中的利率问题,利息=本金×利率×期数.
存款利率问题中有不少有关联的量,如本金、利息、利率等,只有了解它们的相互联系才能解决好此类问题.
15. 解:设这批夹克每件的本钱价为x元,则标价为x元.
依据题意,得x×80%=60.
解得x=50.
答:这批夹克每件的本钱价是50元.
先用本钱价表示出标价,然后依据等量关系:标价×80%=60,列出方程即可.
按标价8折供应即按标价的80%供应.解题时要依据题意列出相应的等量关系式.
《3.2 一元一次方程的应用》提升训练
1. 某旅游社组织200人到怀集和德庆旅游,到德庆的人数比到怀集的人数的2倍少1人,则到德庆旅游的人数为.
A.67人 B.68人 C.133人 D.135人
2. 某湿地公园举行观鸟节活动,全价票为20元/人,半价票为10元/人,该公园共售出1200张门票,得总票款20000元.则半价票售出.
A. 800张 B. 400张 C. 1200张 D. 200张
3. 某品牌羽绒棉服按本钱提升50%后标价,因为换季,企业决定降价销售,营销手段为:买一件打八折,买两件或两件以上打七折.已知客户买一件企业能获利28元,若客户同时买两件,企业每件还能获利元.
A.6 B.7 C.8 D.9
4. 在长为10 m,宽为8 m的长方形空地中,沿平行于长方形各边的方向分割出三个一模一样的小长方形花圃,其示意图如图所示.则小长方形花圃的长和宽分别为.
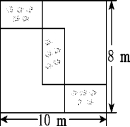
A.3.5m,3m B.3.4m,3.2m
C.4.5m,1m D.4m,2m
5. 一艘船从甲码头到乙码头顺时尚驶用4小时,从乙码头到甲码头逆时尚驶用4小时40分钟,已知水流速度为3千米/小时,则船在静水中的平均速度是.
A.39千米/小时 B.40千米/小时
C.43千米/小时 D.45千米/小时
6. 某商店两个进价不一样的豆浆机都卖378元,其中一个盈利40%,另一个亏本20%,在这次交易中,这家商店是.
A.盈利13.5元 B.亏损13.5元
C.盈利10.5元 D.亏损10.5元
7. 在甲处劳动的有27人,在乙处劳动的有19人,目前另调20人去支援,使在甲处的人数为在乙处人数的2倍,应调往甲、乙两处各.
A.15人,5人 B.16人,4人
C.17人,3人 D.18人,2人
8. 一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
9. 李明以两种方法储蓄了500元钱,一种方法储蓄的年利率是5%,另一种是4%,一年后得利息23元5角,问两种储蓄各存了多少元钱?
10. 某种中药含有甲、乙、丙、丁四种草药成分,其水平比是0.7:
1:2:4.7,现要配制这种中药2100克 ,四种草药分别需要多少克?
答案和分析
【答案】
1. C 2. B 3. B 4. D 5. A 6. A 7. C
8. 亏损8元.
9. 年利率是5%和4%的储蓄分别存了350元和150元.
10. 需要甲种草药175克,乙种草药250克,丙种草药500克,丁种草药1175克.
【分析】
1. 解:设到怀集旅游的人数为x人,则到德庆旅游的人数为人.
依据题意,得x+=200.
解得,x=67,
则到德庆旅游的人数为2×67-1=133.
答:到怀集旅游的人数为67人,到德庆旅游的人数为133人.
故选C.
借助“到德庆的人数比到怀集的人数的2倍少1人”为相等关系列出方程.设到怀集旅游的人数为x人,则到德庆旅游的人数为人,由“某旅游社组织200人到怀集和德庆旅游”,即可用含x的式子表示出来.
本题解题的重点在于依据已知条件确定两者的数目关系,然后列出方程解题.
2. 解:设全价票售出x张,则半价票售出张.
依据题意,得20x+10×=20000,
解方程,得x=800.
1200-x=1200-800=400.
答:全价票售出800张,半价票售出400张.
故选B.
由“该公园共售出1200张门票”,设全价票售出x张,则半价票售出张.依据全价票款+半价票款=总票款,就能打造起方程.
本题解题的重点在于依据已知条件确定两者的数目关系,然后列出方程解题.
3. 解:设该品牌羽绒棉服的本钱价为x元,
依据题意,得80%×x-x=28,
解得,x=140,
则140××70%-140=7.
答:若客户同时买两件,企业每件能获利7元.
故选B.
本题中设该品牌羽绒棉服的本钱价为x元,则该羽绒棉服的标价为x,依据买一件打八折,并且客户买一件企业能获利28元,可以打造起方程. 求出羽绒棉服的本钱价后,依据收益=实质价格-进价,即可求出同时买两件企业每件的获利状况.
4. 解:设小长方形的长为x m,则宽为m.
由题意得,x+2=8,
解得,x=4.
所以,10-2x=2.
答:小长方形花圃的长为4 m,宽为2 m.
故选D.
本题运用了数形结合思想,将图形中存在的等量关系,通过列一元一次方程反映出来,进而解决所求问题.注意挖掘图形中隐含的等量关系是解题的重点.
5. 解:设船在静水中的平均速度是x千米/小时,
依据题意,得4=![]() ,
,
解得,x=39.
答:船在静水中的平均速度是39千米/小时.
故选A.
船在顺水中的速度=船在静水中的速度+水的速度,船在逆水中的速度=船在静水中的速度-水的速度.依据船在顺水中的速度×船在顺水中行驶的时间=船在逆水中的速度×船在逆水中行驶的时间,列出方程解题.
6. 解:设盈利40%的豆浆机进价为x元,
由题意可,得x=378,
解得,x=270.
设亏本20%的豆浆机进价为y元,
由题意,得y=378,
解得,y=472.5.
所以这两个豆浆机的进价和是270+472.5=742.5,
而这两个豆浆机共卖了378×2=756,
由此可知这两个豆浆机共盈利756-742.5=13.5.
答:在这次交易中,这家商店盈利,盈利13.5元.
故选A.
两个豆浆机共卖了378×2=756,是盈利还是亏本要看这家商店进这两个豆浆机时一共花了多少钱.进价高于价格就亏本,进价低于价格就盈利,故要分别计算出这两个豆浆机的进价.
7. 解:设应调往甲处x人,则调往乙处人,
依题意,得27+x=2[19+],
解得,x=17.
所以,20-x=20-17=3.
答:应调往甲处17人,调往乙处3人.
故选C.
本题中的等量关系为:调入后甲处人数=调入后乙处人数的2倍.
本题运用直接设元法求解.调配问题是依据调配后的关系列方程的,剖析是如何调配的,特别应该注意是彻底调走了,还是调到有关的地方去了.
8. 解:设盈利25%的那件衣服的进价是x元,它的产品收益就是0.25x元,
依据进价与收益的和等于价格,得x+0.25x=60.
解得,x=48.
类似地,可以设另一件衣服的进价为y元,它的产品收益是-0.25y元,得y-0.25y=60.
解得,y=80.
两件衣服的进价是x+y=128元,而两件衣服的价格是60+60=120元,
进价大于价格,由此可知卖这两件衣服总共亏损8元.
两件衣服共卖了120元,是盈是亏要看这家商店买进这两件衣服时花了多少钱,假如进价大于价格就亏损,反之就盈利.假设一件产品的进价是40元,假如卖出后盈利25%,那样产品收益是40×25%元;假如卖出后亏损25%,产品收益是40×元.
9. 解:设年利率是5%的储蓄了x元,另一种是4%的储蓄存了元,
依据题意,得x×5%×1+×4%×1=23.5.
解这个方程,得x=350.
所以500-x=150.
答:年利率是5%和4%的储蓄分别存了350元和150元.
本题考查的是本金问题,题目中有两个待求的未知数,大家可以设出一个,另一个未知数借用题目条件用第一个未知数表示出来.
解决储蓄问题的重点在于对关系式的正确运用,利息=本金×利率×期数.
10. 解:设需要甲种草药0 .7x克,乙种草药x克,丙种草药2x克,丁种草药4.7x克,
依据题意,得0.7x+x+ 2x+4.7x=2100.
解得,x=250,
所以,0.7x=175 ,2x=500,4.7x=1175.
答:需要甲种草药175克,乙种草药250克,丙种草药500克,丁种草药1175克.
借助甲、乙、丙、丁四种草药成分的和等于2100克为相等关系列出方程.设其中一份为x克,由甲、乙、丙、丁四种草药的水平比,即可用含x的式子表示出来.
比率分配问题中的全部数目=各种成分的数目值之和.
《3.2 一元一次方程的应用》培优训练
1. 小明和他的哥哥早晨起来沿长为400 m的环形跑道训练跑步,小明跑2圈用的时间和他的哥哥跑3圈用的时间相等,两人同时同地同向出发,经过2 min 40 s他们首次相遇,若他们两人同时同地反向出发,则经过秒他们首次相遇?
A.28 B.32 C.35 D.38
2. 一个水池有甲、乙、丙三个水管,甲、乙是进水管,丙是出水管,单开甲管20分钟可将水池注满,单开乙管15分钟可将水池注满,单开丙管25分钟可将满池水放完.目前先开甲、乙两管,4分钟后关上甲管开丙管,又经过分钟才能将水池注满.
A.15 B.18 C.20 D.23
3. 某国进行足球赛共赛8轮,胜一场得3分,平一场得1分,负一场得0分.在这次足球联赛中,猛虎队平的场数是负的场数的2倍,且8场比赛共得17分,该队共胜场.
A.5 B.6 C.7 D.8
4. 甲、乙两人在一条长400米的环形跑道上跑步,甲的速度为360米/分,乙的速度是240米/分.
两人同时同地同向跑,问首次相遇时,两人一共跑了多少圈?
两人同时同地反向跑,问几秒后两人首次相遇?
5. 足球比赛的得分规则:胜一场得3分,平一场得1分,负一场得0分.一支足球队在某个赛季共需比赛14场.现已比赛8场,负了一场,共得17分.
前8场比赛中,这支球队胜了几场?
这支球队打满14场,最高能得多少分?
通过对比赛状况的剖析,这支球队打满14场比赛,得分高于29分,就可达到目的.请你剖析一下,在后面的6场比赛中,这支球队至少要胜几场,才能达到预期的目的?
答案和分析
【答案】
1. B 2. C 3. A
4. 两人一共走了5圈; 40秒后两人首次相遇.
5. 前8场比赛中,这支球队胜了5场;
打满14场比赛最高能得35分;
后面的6场比赛中,这支球队至少要胜3场,才能达到预期的目的.
【分析】
1. 解:设小明的速度为x m/s,则他的哥哥的速度为![]() m/s,
m/s,
由题意得:
160x=160×![]() x-400,
x-400,
解得,x=5.
则小明的哥哥的速度为5×![]() =7.5,
=7.5,
设经过y s他们首次相遇,
由题意,得:y=400.
解得,y=32.
答:经过32 s他们首次相遇.
故选B.
相等关系:小明跑的路程=哥哥跑的路程-400 m. 本例在求小明及哥哥的速度时,也可设他们两人的速度分别为2x m/s和3x m/s. 环形运动问题中的等量关系:①同向相遇:首次相遇时快者的路程-首次相遇时慢者的路程=跑道一圈的长度;②反向相遇:首次相遇时快者的路程+首次相遇时慢者的路程=跑道一圈的长度.
2. 解:设又经过x分钟才能将水池注满,
依据题意得:![]() ,
,
解得,x=20.
答:又经过20分钟才能将水池注满.
故选C.
在一些工程问题中,工作量未知而又不求工作量时,大家常常把工作量看成整体“1”.设又经过x分钟才能将水池注满,列表如下:
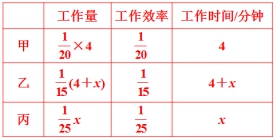
等量关系:甲注水量+乙注水量-丙放水量=1.
本题等量关系的实质是:总工作量等于各部分工作量之和;只是大家要把丙工作量看成“-”工作量.
3. 解:设该队负x场,则平的场数为2x,胜的场数为,
依据题意,得3+2x=17,
解得,x=1.
所以,8-x-2x=8-1-2=5.
答:该队共胜了5场.
故选A.
题中等量关系是:胜场积分+平场积分=17.此类问题使用设间接未知数的办法,设某种场数为x,则其余两种场数都可以用含x的式子表示出来,从而可借助相等关系列方程.
4. 解:设x分钟后两人首次相遇,
由题意,得360x-240x=400.
解得,x=![]() .
.
÷400=5.
答:两人一共走了5圈.
设x分钟后两人首次相遇,
由题意,得360x+240x=400.
解得,x=![]() .
.
![]() 分钟=40秒.
分钟=40秒.
答:40秒后两人首次相遇.
题实质上是追及问题,两人首次相遇,事实上就是快者比慢者多跑一圈,其等量关系是追上时,甲走的路程-乙走的路程=400米;题实质上是相遇问题,两人首次相遇就是两人所走的路程之和为环行跑道一圈的长,其等量关系是相遇时,甲走的路程+乙走的路程=400米.
环形问题中的等量关系:
两个人同地背向而行:相遇问题,甲的行程+乙的行程=一圈周长;两个人同地同向而行:追及问题,甲的行程-乙的行程=一圈周长.
5. 解:设前8场比赛中,这支球队胜了x场,则平了场.
由题意,得3x+×1=17,
解得,x=5.
答:前8场比赛中,这支球队胜了5场.
要使得分最高,需要在后面的几场比赛中全胜,
因此,打满14场比赛最高能得17+×3=35.
设后面的6场比赛中,这支球队至少要胜y场,则平场.
由题意,得3y+×1=29-17,
解得,y=3.
答:后面的6场比赛中,这支球队至少要胜3场,才能达到预期的目的.
设前8场比赛中,这支球队胜了x场,则平了场.依据8场比赛共得17分,列
出方程即可求出获胜的常数;
要使得分最高,需要在后面的几场比赛中全胜;
理解“至少”的意思是解题的重点.因为比赛结果分为胜、负、平三种,所以要想达到预期的目的,在后面的6场比赛中,负的场数越少时所需要胜的场数越少,由此得到后面的6场比赛中,只能出现胜、平两种比赛结果.







