作业设计模板
教 材 上海九年义务教育课本初一 第一学期 (试用本)
课 题 11.3旋转对称图形和中心对称图形
一.课堂训练
试 题 | 解 答 | 设计意图 |
A组 (课本P102/1)
1.一个四叶风车,它的旋转角是多少度?每叶最少旋转多少度可以与其它叶重合?
|
1.它的旋转角是90 o、 180 o、270 o,每一个叶片最少旋转90 o可以与其它叶片重合. 指导学生察看叶片上OA绕着点O旋转到OB时的夹角即为最小的旋转角.
|
加深学生对旋转对称图形和旋转角定义的理解. 强调旋转对称图形的旋转角要小于360o.
|
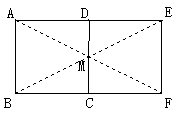
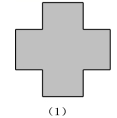
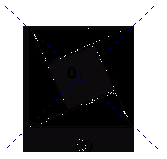
2.如图,什么是旋转对称图形,什么是中心对称图形? (课本P102/2)
(4)
| 2.图形(1)是旋转对称图形,也是中心对称图形.它的旋转中心是直线AB、CD的交点O
图形(2)是旋转对称图形,也是中心对称图形.它的旋转中心是对角线的交点O
图形(3)是旋转对称图形,也是中心对称图形.它的旋转中心是对角线的交点O
图形(4)是旋转对称图形,但不是中心对称图形.它的旋转中心是点O
|
加深学生对旋转对称图形和中心对称图形定义的理解.
|
B组 1.画出一个旋转角为120°的旋转对称图形,它是不是为中心对称图形?(课本P102/3)
| 1.等边三角形是旋转角为120°的旋转对称图形,它不是中心对称图形
正六边形是旋转角为 120°的旋转对称图形,它是中心对称图形. | 旋转角为120 o的旋转对称图形可能不是中心对称图形,如有三个叶片的风扇、正三角形等不是中心对称图形.而正六边形的旋转角可以是120度,并且是中心对称图形. 引导学生进一步理解旋转对称图形和中心对称图形有什么区别与联系. 联系:两种图形都是把一个图形绕着一个定点旋转一个角度后,与初始图形重合. 中心对称图形是旋转对称图形的特例. 不同:当旋转角为180o时,这个图形是中心对称图形,
|
2.下列电子显示屏上的数字什么是中心对称图形?(补充)
| 2.数字 是中心对称图形.
| 感受中心对称图形在日常的应用,进一步认识中心对称图形. |
C组
| 由于△OPR逆时针旋转到与△OBC时,点O的地方没变化,所以旋转中心是点O. 由于点C、R是对应点, ∠ROC是旋转角, 所以 ∠ROC=∠BOC—∠BOR = | 复习巩固旋转中心、旋转角等定义,感知后续学习的几何图形的运动. |
二.课后作业
试 题 | 解 答 | 设计意图 |
A组 1.下图是否一个旋转对称图形?若是,请说出最小的旋转角的大小.
2.下列各图是选自历届世博会徽中的图案,其中是中心对称图形的是( )
A、 B、
|
答:这个图形是旋转对称图形,最小的旋转角是
2.答案(D) | 进一步加深学生对旋转对称图形和旋转角定义的理解.感受旋转对称图形在日常的应用.
进一步加深学生对中心对称图形定义的理解.感受中心对称图形的美.
|
3.如图,假如四边形CDEF旋转后能与正方形ABCD重合,那样图形所在的平面可以作旋转中心的点共有几个?分别进行说明,此时它的旋转角是几度?
|
可以作为旋转中心的点有3个,它们是点C、点D和线段CD的中点M. 以点C为旋转中心时,图形围绕点C,逆时针旋转 以点D为旋转中心时,图形围绕点D顺时针旋转 以M为旋转中心时,图形围绕点M顺时针或逆时针旋转
| 进一步加深学生对旋转对称图形和中心对称图形定义的理解.复习巩固旋转中心和旋转角的定义,培养思维的完整性,学习分类讨论的数学办法.
|
B组 1.如图,4张扑克牌放在桌上,现将它中的某一张在原地旋转
|
1.旋转的是第一张牌,其它三张牌中间的图形不是中心对称图形,所以旋转后在桌上看到的牌中的图形不可以和原先的完全相同.
| 引导学生进一步理解旋转对称图形和中心对称图形有什么区别与联系.感受旋转对称图形在日常的应用.
|
2.画一个旋转角是
| 2.正方形是旋转角为90°的旋转对称图形,它是中心对称图形,正八边形也是旋转角为90°的旋转对称图形,它也是中心对称图形.
| 引导学生进一步理解旋转对称图形和中心对称图形有什么区别与联系.
|
C组 1.下列26个英文大写字母中,是中心对称图形的__________. (补充) ABCDEFGHIJKLMNOPQRSTUVWXYZ |
1.字母HINOSXZ是中心对称图形.
| 进一步加深对中心对称图形定义的理解.感受中心对称图形在日常的应用.
|
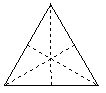
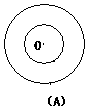
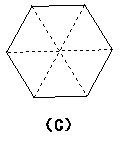
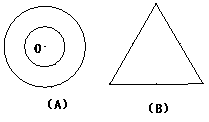
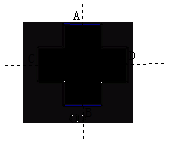
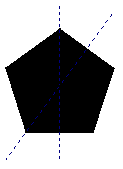
2.下面四个图形都是旋转对称图形.(补充) (1)请指明它们的旋转中心并说明它们的旋转角是多少度? (2)说一说它们什么不是中心对称图形?
|
图(A)的旋转中心就是圆心O,圆旋转任意角度都与它本身重合,圆有旋转不变形.
图(B)的旋转中心是任意两条高的交点,它的旋转角是
图(C)的旋转中心是任意两条对角线的交点,它的旋转角是
图(D)的旋转中心是两条对边的中点连线的交点,
图形B不是中心对称图形.
|
进一步加深学生对旋转对称图形和中心对称图形定义的理解.复习巩固旋转中心和旋转角的定义,培养思维的完整性.
|








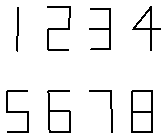
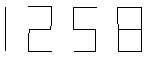
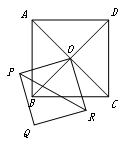 如图,已知正方形ABCD和正方形OPQR,△OPR逆时针旋转后能与△OBC重合,已知∠BOR=55°.则旋转中心是__________,旋转角为__________ 度.(补充)
如图,已知正方形ABCD和正方形OPQR,△OPR逆时针旋转后能与△OBC重合,已知∠BOR=55°.则旋转中心是__________,旋转角为__________ 度.(补充) 



 C、 D、
C、 D、