椭圆
1．（2019全国I理10）已知椭圆C的焦点为
，过F2的直线与C交于A，B两点．若
，
，则C的方程为
A．
B．
C．
D．
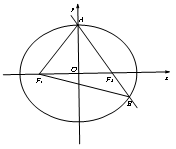
分析 如图所示，设
，则
，所以
.
由椭圆概念
，即
.
又
，，所以
.
因此点A为椭圆的上顶点，设其坐标为
.
由
可得点B的坐标为.
由于点B在椭圆
上，所以.
解得.又
，所以
.所以椭圆方程为
.故选B.
2.（2019北京理4）已知椭圆
的离心率为
，则
（A） （B）
（C）
（D）
分析 由题意，
，得，则
，
所以
，即
．故选B．
3.（2019全国III理15）设
为椭圆C:
的两个焦点，M为C上一点且在第一象限.若
为等腰三角形，则M的坐标为___________.
分析 设，，椭圆C：
的，，
，
，因为M为C上一点且在第一象限，可得
，为等腰三角形，可能或，
即有
，即
，；
，即，舍去．可得
.
4．已知，
是椭圆
的左，右焦点，
是
的左顶点，点在过且斜率为
的直线上，
为等腰三角形，，则的离心率为
B． C．
D．
D【分析】由题意可得椭圆的焦点在轴上，如图所示，
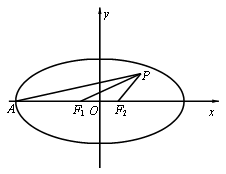
设，所以为等腰三角形，且，
∴，∵
，∴点坐标为，即点．∵点在过点，且斜率为的直线上，
∴
，解得．∴，故选D．
5．（2017新课标Ⅲ）已知椭圆：
的左、右顶点分别为，
，且以线段为直径的圆与直线相切，则的离心率为
A． B．
C． D．
A【分析】以线段为直径的圆是
，直线与圆相切，所以圆心到直线的距离
，整理为，
即
，即 ，，故选A．
6．已知O为坐标原点，F是椭圆C：的左焦点，A，B分别为C的左，右顶点．P为C上一点，且PF⊥x轴．过点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则C的离心率为
A． B． C． D．
A【分析】设，则直线的方程为
，由题意可知，
和
三点共线，则，化简得
，则的离心率．故选A．
