__________
专题12 圆的有关性质与计算
__________
【考试知识点1】垂径定理
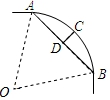
【例1】（2019·湖北中考考试真题）如图，一条公路的转弯处是一段圆弧
，点
是这段弧所在圆的圆心，
，点
是
的中点，且
，则这段弯路所在圆的半径为（）
A．
B． C．
D．
【答案】A
【分析】
【剖析】
依据题意，可以推出AD＝BD＝20，若设半径为r，则OD＝r﹣10，OB＝r，结合勾股定理可推出半径r的值．
【解析】
解：
，
，
在
中，
，
设半径为
得：
，
解得：，
这段弯路的半径为
故选：A．
【点睛】
本题主要考查垂径定理的应用、勾股定理的应用，重点在于设出半径为r后，用r表示出OD、OB的长度．
【变式1-1】（2019·四川中考考试真题）如图，AB，AC分别是⊙O的直径和弦，
于点D，连接BD，BC，且
，
，则BD的长为（ ）
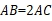
A．
B．4 C．
D．4.8
【答案】C
【分析】
【剖析】
先依据圆周角定理得∠ACB=90°，则借助勾股定理计算出BC=6，再依据垂径定理得到，然后借助勾股定理计算BD的长．
【解析】
∵AB为直径，
∴
，
∴
，
∵，
∴，
在
中，．
故选C．
【点睛】
本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了垂径定理．
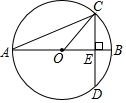
【变式1-2】（2019·四川中考考试真题）如图，
的直径垂直于弦
，垂足是点，
，
，则的长为
A．
B．
C．6 D．12
【答案】A
【分析】
【剖析】
先依据垂径定理得到
，再依据圆周角定理得到
，可得为等腰直角三角形，所以，从而得到的长．
【解析】
∵，AB为直径，
∴，
∵∠BOC和∠A分别为所对的圆心角和圆周角，∠A=22.5°，
∴
，
∴为等腰直角三角形，
∵OC=6，
∴
，
∴
.
故选A．
【点睛】
本题考查了垂径定理及圆周角定理，在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半；垂直于弦的直径，平分这条弦且平分这条弦所对的两条弧．
【考试知识点2】弧、弦、圆心角之间的关系
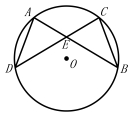
【例2】（2019·四川自贡中考考试真题）如图，⊙中，弦与相交于点,
,连接.
求证：⑴
；
⑵.
【答案】（1）见分析；（2）见分析.
【分析】
【剖析】
（1）由AB=CD知
，即，据此可得答案；
（2）由知AD=BC，结合∠ADE=∠CBE，∠DAE=∠BCE可证△ADE≌△CBE，从而得出答案．
【解析】
证明（1）∵AB=CD，
∴，即，
∴；
（2）∵，
∴AD=BC，
又∵∠ADE=∠CBE，∠DAE=∠BCE，
∴△ADE≌△CBE（ASA），
∴AE=CE．
【点睛】
本题主要考查圆心角、弧、弦的关系，圆心角、弧、弦三者的关系可理解为：在同圆或等圆中，①圆心角相等，②所对的弧相等，③所对的弦相等，三项“知一推二”，一项相等，其余二项皆相等．
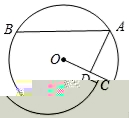
【变式2-1】（2018·黑龙江中考考试真题）如图，在⊙O中，，AD⊥OC于D．求证：AB=2AD．
【答案】证明见分析
【分析】
【剖析】
延长AD交⊙ O于E,可得、AB=AE，可得出结论.
【解析】
延长AD交⊙O于E，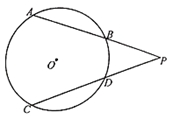
∵OC⊥AD，
∴
，AE=2AD，
∵
，
∴，
∴AB=AE，
∴AB=2AD．
【点睛】
本题主要考查垂径定理及弧、弦、圆心角之间的关系，灵活做辅助线是解本题的重点.
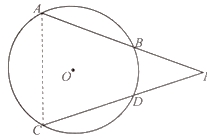
【变式2-2】（2019·江苏中考考试真题）如图，⊙O的弦AB、CD的延长线相交于点P，且AB＝CD．求证PA＝PC．
【答案】见分析.
【分析】
【剖析】
连接AC，由圆心角、弧、弦的关系得出
，进而得出
，依据等弧所对的圆周角相等得出∠C＝∠A，依据等角对等边证得结论．
【解析】
解：如图，连接.
∵，
∴.
∴，即.
∴
.
∴.
【点睛】
本题考查了圆心角、弧、弦的关系，圆周角定理，等腰三角形的断定等，熟练学会性质定理是解题的重点．
【考试知识点3】圆周角定理及其推论
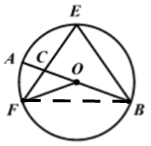
【例3】（2019·陕西中考考试真题）如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF=EB，EF与AB交于点C，连接OF，若∠AOF=40°，则∠F的度数是（ ）
A．20° B．35° C．40° D．55°
【答案】B
【分析】
【剖析】
连接FB，由邻补角概念可得∠FOB=140°，由圆周角定理求得∠FEB=70°，依据等腰三角形的性质分别求出∠OFB、∠EFB的度数，继而依据∠EFO＝∠EBF-∠OFB即可求得答案.
【解析】
连接FB，
则∠FOB=180°-∠AOF=180°-40°=140°，
∴∠FEB＝∠FOB=70°，
∵FO＝BO，
∴∠OFB＝∠OBF=÷2=20°，
∵EF＝EB，
∴∠EFB＝∠EBF=÷2=55°，
∴∠EFO＝∠EBF-∠OFB=55°-20°=35°，
故选B.
【点睛】
本题考查了圆周角定理、等腰三角形的性质等常识，正确添加辅助线，熟练学会和灵活运用有关常识是解题的重点.
【变式3-1】（2019·北京中考考试真题）已知锐角∠AOB如图，（1）在射线OA上取一点C，以点O为圆心，OC长为半径作
，交射线OB于点D，连接CD；
（2）分别以点C，D为圆心，CD长为半径作弧，交于点M，N；
（3）连接OM，MN．
依据以上作图过程及所作图形，下列结论中错误的是（ ）
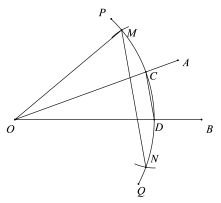
A．∠COM=∠COD B．若OM=MN，则∠AOB=20°
C．MN∥CD D．MN=3CD
【答案】D
【分析】
【剖析】
由作图知CM=CD=DN，再借助圆周角定理、圆心角定理逐一判断可得．
【解析】
解：由作图知CM=CD=DN，
∴∠COM=∠COD，故A选项正确；
∵OM=ON=MN，
∴△OMN是等边三角形，
∴∠MON=60°，
∵CM=CD=DN，
∴∠MOA=∠AOB=∠BON=
∠MON=20°，故B选项正确；
∵∠MOA=∠AOB=∠BON=20°，
∴∠OCD=∠OCM=80°，
∴∠MCD=160°，
又∠CMN=∠AON=20°，
∴∠MCD+∠CMN=180°，
∴MN∥CD，故C选项正确；
∵MC+CD+DN＞MN，且CM=CD=DN，
∴3CD＞MN，故D选项错误；
故选：D．
【点睛】
本题主要考查作图-复杂作图，解题的重点是学会圆心角定理和圆周角定理等要点．
