初中二年级上第十一章三角形单元测试及参考答案（人教版）
（时限：100分钟 总分：100分）
选择题：将下列各题正确答案的代号的选项填在下表中。（每小题2分，共24分。）
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 |
|
|
|
|
|
|
|
|
|
|
|
|
1.如图，△ABC中，∠C＝75°，若沿图中虚线截去∠C，则∠1＋∠2＝（ ）
A. 360° B. 180° C. 255° D. 145°
2.若三条线段中a＝3，b＝5，c为奇数，
那样由a，b，c为边组成的三角形共有（ ）
A. 1个 B. 3个
C. 无数多个 D. 没办法确定
3.有四条线段，它们的长分别为1cm，2cm，3cm，4cm，
从中选三条构成三角形，其中正确的选法有（ ）
A. 1种 B. 2种 C. 3种 D. 4种
4.能把一个三角形分成两个面积相等的三角形是三角形的（ ）
A. 中线 B. 高线 C. 角平分线 D. 以上都不对
5.假如一个三角形的三条高的交点恰是三角形的一个顶点，那样这个三角形是（ ）
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D.不可以确定
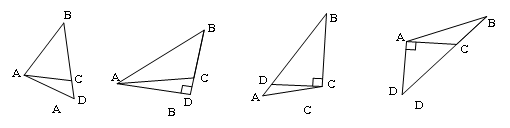
6.在下列各图形中，分别画出了△ABC中BC边上的高AD，其中正确的是（ ）
7.下列图形中具备稳定性的是（ ）
A. 直角三角形 B. 正方形 C. 长方形 D. 平行四边形
8.如图，在△ABC中，∠A＝80°，∠B＝40°.D、E分别是AB、AC上的点，且DE∥BC，则∠AED的度数是（ ）
A.40° B.60° C.80° D.120°
9.已知△ABC中，∠A＝80°，∠B、∠C的平分线的夹角是（ ）
A. 130° B. 60° C. 130°或50° D. 60°或120°
10.若从一多边形的一个顶点出发，最多可引10条对角线，
则它是（ ）
A.十三边形 B.十二边形 C.十一边形 D.十边形
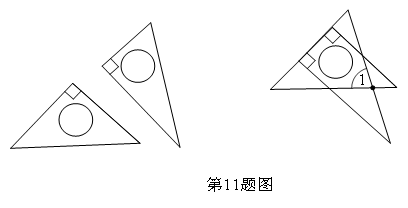
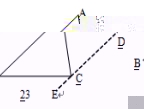
11.将一副直角三角板如图放置，使含30°角的三角板的一条直角边和45°角的三角板的一条直角边重合，则∠1的度数为（ ）
A.45° B.60° C.75° D.85°
12.用三个不一样的正多边形可以铺满地面的是（ ）
A. 正三角形、正方形、正五边形 B. 正三角形、正方形、正六边形
C. 正三角形、正方形、正七边形 D. 正三角形、正方形、正八边形
2、填空题：（本大题共8小题，每小题3分，共24分。）
13.三角形的内角和是__________，n边形的外角和是__________.
14.已知三角形三边分别为1，x，5，则整数x＝__________.
15.一个三角形的周长为81cm，三边长的比为2︰3︰4，则最长边比最短边长__________.
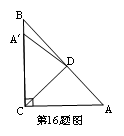16.如图，
中，∠ACB＝90°，∠A＝50°，将它折叠，使点A落在边CB上的A/处，折痕为CD，则∠A/DB＝__________
17.在△ABC中，若∠A︰∠B︰∠C＝1︰2︰3，
则∠A＝__________，∠B＝__________，∠C＝__________.
18.从n（n＞3）边形的一个顶点出发可引__________条对角线，
它们将n边形分为__________个三角形.
19.已知一个多边形的所有内角与它的一个外角之和是2400°，那样这个多边形的边数是__________，这个外角的度数是__________.
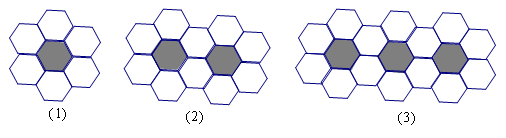
20.用黑白两种颜色的正六边形地砖按图所示的规律镶嵌成若干个图案：
⑴第四个图案中有白色地砖__________块；
⑵第n个图案中有白色地砖__________块.
解答卷：（本大题共52分）
21.（本小题5分）若a，b，c分别为三角形的三边，化简 ：
.
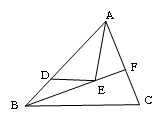22.（本小题5分）如图所示，图中共有多少个三角形？请写出这类三角形并指出所有以E为顶点的角.
23.（本小题5分）证明：三角形三个内角的和等于180°.
已知：△ABC（如图）.
求证：∠A＋∠B＋∠C＝180°.
24.（本小题8分）如图22（1）所示，称“对顶三角形”，其中，∠A＋∠B＝∠C＋∠D，
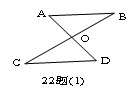借助这个结论，完成下列填空.
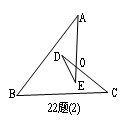
)如图22题，∠A＋∠B＋∠C＋∠D＋∠E＝__________.
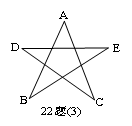
如图22题（3），∠A＋∠B＋∠C＋∠D＋∠E＝__________.
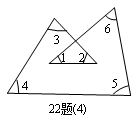
如图22题（4），∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝__________.
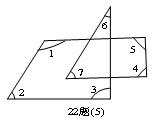
如图22题（5），∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＝__________.
25.（本小题5分）如图所示，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，
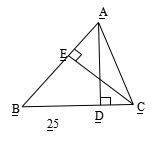已知AB＝6，AD＝5，BC＝4，求CE的长.
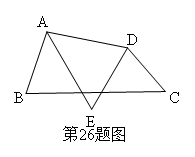
26.（本小题6分）如图，四边形ABCD中，AE平分∠BAD，DE平分∠ADC.
⑴.假如∠B＋∠C＝120°，则∠AED的度数＝__________.（直接写出结果）
⑵.依据⑴的结论，猜想∠B＋∠C与∠AED之间的关系，并说明理由.
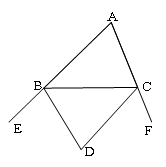
27.（本小题6分）如图所示，∠ACD是△ABC的外角，∠A＝40°，BE平分∠ABC，
CE平分∠ACD，且BE、CE交于点E.求∠E的度数.
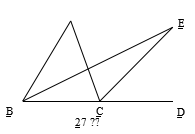
28.（本小题6分）BD、CD分别是△ABC 的两个外角∠CBE、∠BCF的平分线，
求证：∠BDC＝90°－ 
∠A.
29.（本小题6分）如图，在直角坐标系中，点A、B分别在射线OX、OY上移动，BE是∠ABY的角平分线，BE的反向延长线与∠OAB的平分线相交于点C，试问∠ACB的大小是不是发生变化？假如维持不变，请给出证明.
参考答案：
1、1.C；2.B；3.A；4.A；5.C；6.B；7.A；8.B；9.C；10.A；11. ；12.B；
2、13.180°、360°；14. 5；15. 18cm；16. 10° ；17. 30°、60°、90°；
18.（n－3）、（n－2）；19. 15、60°；20. ①18、②4n＋2；
3、21.－a＋b＋3c；
22. 图中有7个三角形 三角形有：△ABC, △ADE, △BED,△ABE,△AEF,△ABF,△BFC
以E为顶点的角：∠BEA, ∠BEA∠BEF,∠DEA,∠DEF, ∠AEF
23. 证明：过点C作DE//AB
∴∠ACD=∠A ∠ECB=∠B
∵∠ECB+∠C+∠ACD=180°
∴∠A＋∠B＋∠C＝180°
24.180°180°（补成三角形）360°（补成四边形）540°（补成五边形）
25. 解：同一个三角形的面积不变
∴ ×BC×AD=×AB×CE CE＝
；
26. 解（1）∵ABCD为四边形，内角和为360度
∴∠A+∠D=360°-120°=240°
∵AE平分∠BAD，DE平分∠ADC
∴∠EAD+∠EDA=1/2=120°
∴∠AED=180°-120°=60°
∵ ∠B＋∠C=360°-
∠A+∠D=2
∴∠B＋∠C=360°-=360°-2=2∠AED
∴∠B＋∠C=2∠AED
27. 解：
由于∠ACD是△ABC的外角，∠A＝40°
所以∠ACD＝40°+∠ABC
由于BE平分∠ABC，CE平分∠ACD
所以∠ABC＝2∠EBC, ∠ACD=2∠ECD
所以∠ACD＝40°+∠ABC＝40°+2∠EBC
由于∠E＝∠ECD－∠EBC,
所以∠E＝∠ECD－∠EBC＝1/2∠ACD-1/2∠ABC =1/2=20°
28. 证明：∠CBE、∠BCF为△ABC的外角
所以∠CBE=∠A+∠C ∠BCF=∠B+∠A
∠CBE+∠BCE=∠A+∠C+∠B+∠A=180°+∠A
由于BD、CD分别是△ABC 的两个外角∠CBE、∠BCF的平分线，
所以∠DBC+∠DCB=1/2= ＝90°+∠A
在△BDC中
∠BDC＝180°－（∠DBC+∠DCB）＝180°－（90°+∠A）＝90°－ ∠A.
29. 解：∠C的大小维持不变
理由：
∵∠ABY=90°+∠OAB，AC平分∠OAB，BE平分∠ABY，
∴∠ABE=½∠ABY=½（90°+∠OAB）=45°+½∠OAB，
即∠ABE=45°+∠CAB，
又∵∠ABE=∠C+∠CAB，
∴∠C=45°，
故∠ACB的大小不发生变化，且一直维持45°
