![]() 作业设计
作业设计
教 材 上海九年义务教育课本 初一 第一学期 (试用本)
课 题 9.15十字相乘法(1)
一.课堂训练
试 题 | 解 答 | 设计意图 |
A组 1. 填空 将下列整数表示成两个整数积的形式(尽量多地) 6=__________, 8=__________, -10=__________, -15=__________.(补充) |
6=1 8=1 -10=1 -15=1 |
学生通过训练理解把常数项分解成两数相乘,而且这两数的和恰好等于一次项系数那样就能用十字相乘法. |
2. 分解因式: (1) (2) (3) (4) (5) (6) (课本P52 /1)
|
|
学生训练初步学会分解常数项,当常数项为正数时,可分解为同号两数的积,一次项系数的符号与分解所得两数的符号相同,当常数项为负数时,可分解为异号两数的积,一次项系数的符号取常数项分解所得两数绝对值较大的符号.
|
B组 1.填空 若多项式
|
(1)m=-3 n=-1
(3)24 -2
|
学生进一步学会二次项系数为1的十字相乘法
|
2. 下列各式中,因式分解的结果是 A. (补充) |
D 注:借助因式分解是整式乘法的逆向变形可以把 |
学生学会因式分解是整式乘法的逆向变形 |
3. 分解因式: (1) (2) (补充) |
(1)
|
学生灵活运用十字相乘法解较为复杂的二次三项式因式分解 |
4. 已知二次三项式 (补充) | 解: 注:由于48=1 . | 学生进一步学会 运用十字相乘法分解常数项,使分解所得两数的和等于一次项系数 |
二.课后作业
试 题 | 解 答 | 设计意图 |
A组 1.将下列整数表示成两个整数积的形式(尽量多地) 9=__________, 15=__________, -12=__________, -28=__________. (训练册P32/1) | 9=1 =3 15=1 =3 -12=1 =2 = -28=1 =2 =
| 学生进一步通过训练理解把常数项分解成两数相乘,而且这两数的和恰好等于一次项系数那样就能用十字相乘法. |
2. k为下列各数时,请将关于x的多项式 (1)k=11; (2)k=-7 (训练册P32/2) |
(1)当k=11时 = (2)当k=-7时 = | |
3.分解因式 (1) (2) (3) (4) (6) (7) (8) (训练册P32/3) |
答: (1) (2) (3) (4) (5) (6) (7) (8) |
学生进一步训练巩固运用十字相乘法进行二次三项式因式分解,并总结常数项的符号与分解所得因式常数项的符号与原二次三项式一次项系数的符号的关系.
|
4.注意观察上题分解前后系数、常数的符号特点,回答问题: (1)当二次三项式中常数项为正数时,分解所得因式中常数项的符号有什么关系?分解所得因式中常数项的符号与原二次三项式中一次项系数的符号有什么关系? (2)当二次三项式中常数项为负数时,分解所得因式中常数项的符号有什么关系?分解所得因式中常数项的符号与原二次三项式的符号有什么关系? (训练册P32/4) |
答:(1)当二次三项式中常数项为正数时,分解所得因式中常数项是同号;分解所得因式中常数项的符号与原二次三项式中一次项系数的符号也是同号 (2)当二次三项式中常数项为负数时,分解所得因式中常数项是异号;分解所得因式中常数项的符号与原二次三项式的符号不可以确定,但分解所得因式中常数项的符号与原二次三项式中一次项系数的符号同号 | |
B组 1.若 A.-3 B.-1 C.1 D.3 (补充)
|
A 由于6=3 有-m=5,即m= -5,所以 |
学生进一步运用十字相乘法求二次三项式的一次项系数及分解因式的常数项.
|
2. 分解因式: (1) (2) (补充) |
(1)
(2)
| 学生灵活运用十字相乘法解较为复杂的二次三项式因式分解. |
3. 求整数n,可以使二次三项式
| 答: 注:由于24=1 2
| 学生进一步巩固运用十字相乘法分解常数项,因式分解所得两数的和等于一次项系数. |




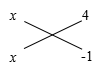 解:
解: 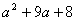 (
(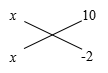 (3)
(3)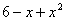 (4).
(4). (5)
(5)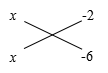 (6).
(6).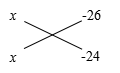 解:
解: 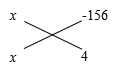 (2)
(2)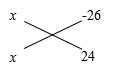 解:
解: