控江中学2018-2019学年度第一学期9月份高中三年级开学考数学试题
1、填空题。
1.已知集合
则
__________.
2.方程
的解为_________.
3.若
,则它的反函数是
________.
4.设
为单位向量,且互相垂直,若
，则向量在方向上的投影为_____________.
5.已知某圆锥体的底面半径为,沿圆锥体的母线把侧面展开后得到一个圆心为
的扇形,则该圆锥体的母线长是__________.
6.设函数若
,且
,则实数构成的集合为________.
7.在无穷等比数列
中,
,则
____________.
8.设
分别双曲线
的左右焦点,若在双曲线右支上存在点P满足
,则该双曲线的渐近线方程是_______________.
9.函数
的值域是_____________.
10.甲、乙、丙三人相互传球,首次由甲将球传岀,毎次传球时,传球者将球等可能地传另外两人中的任何一人,经过三次传球后,球仍在甲手中的概率是__________.
11.已知函数
对任意都有
,且
是增函数,则用列举法表示函数的值域是____________.
12.设常数
,无穷数列满足
若存在常数
,使得对于任意
,不等式
恒成立,则的最大值是_________.
2、选择题。
13.若函数
,则该函数在上是
A.单调递减无最小值 B.单调递减有最小值
C.单调递增无最大值 D.单调递增有最大值
14.“
”是“实系数一元二次方程
有虚根”的______条件.
A.必要非充分 B.充分非必要 C.充分必要 D.非充分非必要
15.全集为R,集合
则集合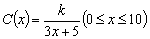可表示为
A.
B.
C.
D.
16.已知
,若
,则对此不等式描述正确的是
A.若
,则至少存在一个以
为边长的等边三角形
B.若
,则对任意满足不等式的都存在以为边长的三角形
C.若,则对任意满足不等式的都存在以为边长的三角形
D.若
,则对满足不等式的没有以为边长的直角三角形
3、解答卷
17.在正三棱柱
中,已知,求：
异面直线
与
所成角的大小；四棱锥
的体积。
18.为了在夏天降温和冬天供暖时降低能源损耗,房子的屋顶和外墙需要建造隔热层。某幢建筑物要建造可用20年的隔热层,毎厘米厚的隔热层建导致本为6万元,该建筑物每年的能源消耗成本C与隔热层厚度满足关系：，若不建隔热层,每年能源消耗成本为8万元,设为隔热层建造成本与20年的能源消耗成本之和。
求的值及的表达式；
隔热层修建多厚时,总成本达到最小,并求最小值。
19.已知函数的图像上的一个最高点
,与该最高点近期的一个最低点是
.
求函数的分析式及其单调递增区间；
在△BC中,角A、B、C所对的边分别为,且
,角A取值范围是区间M,当时,试求函数的取值范围.
20.设实数
,椭圆
的右焦点为F,过F且斜率为的直线交D于P、Q两点,若线段PQ的中点为N,点O是坐标原点,直线ON交直线
于点M.
若点P的横坐标为1,求点Q的横坐标；
求证:MF⊥PQ；
求的最大值.
21.设为正整数,集合
，对于集合
中的任意元素
记
.
当时,若,求
和的值；
当时,设B是A的子集,且满足:对于B中的任意元素
,当相同时,是奇数；当不同时,是偶数，求集合B中元素个数的最大值；
给定不小于2的,设B是A的子集,且满足:对于B中的任意两个不一样的元素，
.写出一个集合B,使其元素个数最多,并说明理由。
