正比率函数与反比率函数习题
一级题
1、填空题：
表示两个比________的式子，叫做比率。
在比率中，两个外项的积等于两个________的积。
假如4×12=6×8，那样以4和12做内项的一个比率是______：4=12：______。
假如
：
=x：3，那x=______。
假如7x=6y，（y≠0），那样
=______。
假如x：y=z：x，那样x是y与z的____________。
数______和15的比率中项是30。
假如x和y成正比率，且当x=4时，y=28，则y与x之间的函数分析式是___________。
正比率函数y=kx的图象是经过点（________）和点（________）的一条_____线。
10、假如正比率函数y=kx的值随x的增大而增大，那样k的取值范围是__________。
11、函数y=
叫做________函数，它的图象叫做__________，它有______个分支。
12、假如函数y=的图象在2、四象限，那样k的取值范围是__________。
13、在函数y=-
的图象所在的象限内，y随x的增大而________。
14、矩形的面积与长a、宽b之间有关系S=ab，假如长a不变，那样______是自变量，______是函数。
15、“y是x的函数”用函数记号可以表示为__________。
16、函数有__________、__________、__________等三种表示方法。
17、函数y=2x2-5x-3的概念域是____________。
18、函数y=-的概念域是____________。
19、若f=2x-3，则f=________。
20、函数f=-1，叫做__________函数。
21、某仓库有煤1000吨，天天运进80吨，x天后仓库共有煤y吨，则y与x之间的函数关系式是________。
22、在直角三角形中，假如两个锐角分别为x（度）和y（度），那样y关于x的函数分析式是__________。
2、选择题：
1、下列各组比中，可以组成比率的是（ ）
A. 
：和0.4：50% B. ：
和5：6
C. 0.8：0.5和40：25 D. 4：0.9和2：0.3
2、下列各问题中的两个量成正比率的是（ ）
A. 三角形的底边长肯定，它的面积和这底边上的高；
B. 圆锥体积肯定，它的底面积和高；
C. 扇形的半径和面积； D.圆的面积和直径。
3、下列各函数中，是反比率函数的是（ ）
A. y=
－1 B. y=
C. y=4x D. y=x-1
4、下列各函数中，函数值y随x的增大而减小的是（ ）
A. y=
B. y=
C.y=-
D.y=-4x
5、下列各图象中，可能是函数y=kx和y=的大致图象是（ ）
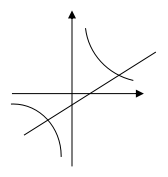
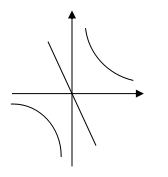
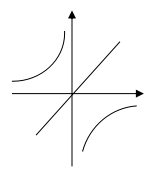
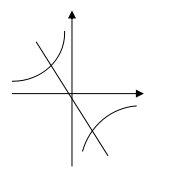
3、解比率（a2－3a＋2）：x=：
4、解答卷
1、已知正比率函数y=kx，当x=5时，y=
，求当x=时，y的值。
2、假如y与x成反比率，并且经过点（3，-2）和点（n，2），求n的值。
3、已知直线y=kx过点（-2，4），问点（1，-2）是不是在这条直线上？为何？
4、已知函数y=
x是反比率函数，求m的值，并求当x为什么值时，y的值是
。
5、已知点A（4，3）在双曲线y=上，（1）求函数y=的分析式；（2）假如点B（m，2m）是这曲线上的一点，求点B的坐标。
5、求下列函数的概念域：
（1） y=
y=-
y=
y=
6、已知：f=
，求f和f。
二级题
填空题
若（x＋2y）：=9：4，则x：y=_________。
若x：=
：
，则x=________。
假如m2=15ab，那样m是5a和________的比率中项。
若
=
，则=________。
若5x=9y，则
=_________。
3和8的比率中项是________。
线段4cm与8cm的比率中项是________。
假如函数y=x是正比率函数，那样m的取值范围是__________。
已知正比率函数y=kx的图象经过点（2t，-t），那样k=________。
10、当k=________时，函数y=kx＋是正比率函数。
11、已知正比率函数y=x，假如当x=2时，y=10，那样当x=________时，y=-15。
12、假如正比率函数y=kx的值随x的增大而减小，那样它的图象经过第______象限。
13、反比率函数y=的图象经过点（4-2，4+2），那样k=________。
14、假如反比率函数y=
的值在图象所在的象限内随x的增大而增大，那样当x=-2时，y______0（填“>”、“=”、或“<”）。
15、反比率函数y=x
在图象所在的象限内，y随x的增大而________。
16、已知正比率函数y=kx的图象经过2、四象限，那样反比率函数y=
的图象在第________象限内。
17、当k________时，函数y=
的值在它的图象所在的每一个象限内，随x的增大而减小。
18、常值函数的图象是__________的一条直线。
19、函数y=
+的概念域是________________。
20、假如函数y=2x的取值范围是-3
21、把x=
写成y=f的形式后是___________。
22、已知F=
，且F=4，则a=________。
23、假如x与y成正比率，y与z成反比率，那样x与z________。
24、在长为20cm，宽为8cm的长方形的纸板上挖了一个直径为xcm的圆形的孔，则剩下的纸板面积y与x之间的函数关系式是________________。
25、一只水箱的容积为20立方米，每小时向这只空箱水箱里注入0.2立方米的水，把水箱注满为止。这个水箱内的水量M（立方米）与时间t（小时）之间的函数关系式为___________________。
26、小明家离学校16千米，他骑车以6千米/小时的速度从家出发去学校，x小时后，小明离学校的距离为y千米，则y与x之间的函数关系式是_______________________。
2、选择题
1、下列各问题中的两个量成反比率的是（ ）
A．正方形的面积和边长； B. 长方形面积肯定,它的长和宽；
C．梯形面积肯定，它的上底和下底；
D．圆柱体积肯定，它的底半径和高。
2、下列说法中，正确的是（ ）
A．函数y=kx是正比率函数；
B．函数y=的值随的增大而减小；
C．函数y=-x的图象经过2、四象限内；
D．函数y=-的图象与轴有一个交点。
3、下列各组函数中，两个函数是相同函数的是（ ）
A．y=x与y=
B.y=
与y=2x
C.y=2与y= D.y=x与y=
4、下列各函数中，图象经过点（-3，2）的是（ ）
A.y=-
x B.y=-
x C.y=-
D.y=
3、解答卷
1、假如函数y=x∣m∣-1为正比率函数，且这个函数的图象经过2、四象限，求该函数的分析式。
2、已知y-3与-2x成正比率，且x=1时，y=2，求当x取何值时，y的值为-1。
3、直线y=2x和双曲线y=都经过点，求：（1）m的值；（2）k的值。
4、函数y=x
是正比率函数。（1）求m的值；（2）假如点P在这正比率函数的图象上，求a的值。
5、已知正比率函数y=x与反比率函数y=的图象都经过点A、B，假如点A的纵坐标是4，求点A、B的坐标。
6、已知反比率函数y=的图象与第一象限的角平分线的交点的横坐标为3，求这正比率函数的分析式，并求当x为什么值上，y的值为＋1。
7、已知y-5与3-x成正比率，且x=1时，y=6，求：（1）y关于x的函数分析式；（2）当x为什么值时，y=-1。
8、已知：y=y1+y2，其中y1与x2成正比率，y2与x成反比率，并且当x=时，y=5；当x=1时，y=-1，求y与x之间的函数关系式。
9、已知：y=y1+y2，且y1与x+1成正比率，y2与x-1成反比率，且当x=2时，y=3；当x=0时，y=5，（1）求y与x之间的函数关系式；（2）求当x=4时，y的值。
10、当m、n为什么值时，函数y=x＋是正比率函数？
11、已知一个正比率函数的图象经过点（6，-3），（1）求这个正比率函数的分析式；（2）假如点M（a，-1）和点N（，-b）也在这个正比率函数的图象上，求a＋b2的值。
12、已知正比率函数y1=k1x和反比率函数y2=
的比率系数k1和k2互为倒数，且正比率函数的图象经过点（2，1），（1）求这两个函数的分析式；（2）假如y=y1+y2，求当时，的值是多少？
13、已知函数x=，试用x的代数式表示y，求出函数的概念域及当x=2时，y的值。
三级题
填空题
函数y=-
上有两点和，假如0
若直线y=x＋k2－4经过原点，则k的值等于___________。
点p在直线y=kx上，点p到x轴和y轴的距离之比为2：3，那样k的值为________。
假如与y成正比率，与z成反比率，则x与z成_______________关系。
等腰三角形的周长为20cm，假如腰长为xcm，底长为ycm，那样y关于x的函数分析式是__________________________。
等腰三角形的周长为20cm，假如底长为xcm，腰长为ycm，那样y关于x的函数分析式是__________________________。
已知：f=，那样当m<1时，f=________________。
2、解答卷
1、在直角坐标系内有点A（-1，0），B（3，0），C（2，m），△ABC的面积为12，直线y=kx经过点C，求直线y=kx的分析式。
2、函数y=的图象经过点A（3，8）和点B（4，m），点C（4，0）是在x轴上的一点，（1）求k、m的值；（2）求四边形OABC的面积。
3、已知，直线y=kx经过点A（5，9）和点B（m，-3），点C（10，0）在x轴上，求这条直线的分析式和△ABC的面积。
4、已知，点P在第二象限，PA⊥x轴，PB⊥y轴，垂足分别为点A、B。OA比OB长1，假如四边形OAPB的周长为18，求经过点0、P的直线的分析式。
5、正比率函数的图象过点（-2，5），过图象上一点A作y轴的垂线，垂足点B的坐标为（0，-3），求点A的坐标和△AOB的面积。
6、已知y=y1-y2，y1与成反比率，y2与成正比率，且当x=1时，y=-1，又当x=3时，y=5，求y关于x的函数分析式，并求当x=时，y的值是多少？
7、等腰梯形的周长为50cm，腰长为10cm，假如这个等腰梯形的上底为xcm，下底为ycm，求y关于x的函数分析式及这个函数的概念域。
8、已知：点P（m,n）在第二象限内，PA⊥y轴于点A，双曲线y=经过点P，假如△OPA的面积为4，（1）求k的值；（2）假如点Q在这条双曲线上，求点Q的坐标。
9、已知：反比率函数y=的图象经过点A（2，4）和点B（4，m），求点B的坐标和△OAB的面积。
11、已知点A在反比率函数y=-的图象上，AB∥x轴，交正比率函数y=2x的图象于点B，点C和点D分别是点A和点B关于原点O的对称点，求出点A、B、C、D的坐标和四边形ABCD的面积。
12、在一块边长为15cm，宽为10cm的长方形铁皮，四角各截去边长为xcm的小正方形，然后将剩下的部分折成一个无盖盒子，（1）写出这个盒子的容积V关于自变量的函数分析式，并说明x的取值范围；（2）当小正方形的边长为2cm时，这个无盖盒子的容积是多少？
13、已知，在△ABC中，∠ABC与∠ACB的平分线交于点O，设∠A=x0,∠BOC=y0,求y1与x之间的函数关系式；又假如∠ABC与∠ACB的外角的平分线交于点P，∠BPC=y20,求y2与x之间的函数关系式。
四级题
1、若函数y=xm2-3m+n＋3m－2n是正比率函数，求m、n的值。
2、已知正比率函数的图象经过点（-4，8）
（1）若点P（a，-1）、Q（，-b）都在图象上，求a、b的值；
（2）若点A在图象上，AB⊥轴，垂足为点（0，-8），求S△OAB。
3、已知：在反比率函数的图象上有不重合的两点A、B， 且A点的纵坐标是2，B点的横坐标是2，BB′和AA′都垂直于轴，B、A为垂足。
（1）求A、B两点的坐标；
（2）求S△OBB′；
（3）当OB=2时，求S△OAB。
4、已知正方形OABC的面积为9，点O为坐标原点，点B，点P是函数y=的图象上的点，过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S。（1）求B点坐标与的值；（2）当S=时，求P点坐标；（3）写出S关于m的函数关系式。
