高中三年级数学拓展课01
1、填空题(1-6题每题4分,7-12题每题5分)
1. 已知全集![]() ,集合
,集合![]() ,则集合
,则集合![]() ____________.
____________.
2. 已知函数![]() ,则方程
,则方程![]() 的解
的解![]() ____________.
____________.
3. 已知线性方程组的增广矩阵为![]() ,若该线性方程组的解为
,若该线性方程组的解为![]() ,则实数
,则实数![]() ____________.
____________.
4. 无穷等比数列![]() 的前
的前![]() 项的和是
项的和是![]() ,且
,且![]() ,则首项
,则首项![]() 的取值范围是____________.
的取值范围是____________.
5. 已知虚数![]() 满足
满足![]() ,则
,则![]() ____________.
____________.
6. ![]() 展开式的二项式系数之和为256,则展开式中
展开式的二项式系数之和为256,则展开式中![]() 的系数为____________.
的系数为____________.
7. 已知![]() 的内角
的内角![]() 、
、![]() 、
、![]() 所对应边的长度分别为
所对应边的长度分别为![]() 、
、![]() 、
、![]() ,若
,若![]() ,则角
,则角![]() 的大小是____________.
的大小是____________.
8. 学校有两个饭店,现有3名学生前往就餐,则三个人不在同一个饭店就餐的概率是____________.
9. 若数![]() 的规范差为2,则数
的规范差为2,则数![]() 的方差为____________.
的方差为____________.
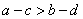 10. 如图,在矩形
10. 如图,在矩形![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且满足
上,且满足![]() ,若
,若![]() ,则
,则![]() ____________.
____________.
11. 已知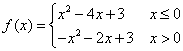 ,当
,当![]() 时不等式
时不等式![]() 恒成立,则实数
恒成立,则实数![]() 的最大值是____________.
的最大值是____________.
12. 已知![]() 是概念在
是概念在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,若直线
,若直线![]() 与函数
与函数![]() 的图像恰有11个不一样的公共点,则实数
的图像恰有11个不一样的公共点,则实数![]() 的取值范围为____________.
的取值范围为____________.
2、选择题(每题5分)
13. 下列四个命题中,为真命题的是( )
A. 若![]() ,则
,则![]() B. 若
B. 若![]() ,则
,则![]()
C. 若![]() ,则
,则![]() D. 若
D. 若![]() ,则
,则![]()
14. 下列函数中,既是奇函数,又在区间![]() 上递增的是( )
上递增的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
15. 设![]() 是两个单位向量,其夹角为
是两个单位向量,其夹角为![]() ,则“
,则“![]() ”是“
”是“![]() ”的( )
”的( )
A. 充分非必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也非必要条件
16. 设![]() 是互不相等的正数,则下列不等式中不恒成立的是( )
是互不相等的正数,则下列不等式中不恒成立的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
3、解答卷
17. (本题满分14分,第1小题8分,第2小题6分)
如图,某人计划做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充。已知金字塔的每一条棱和边都相等。
(1)求证:直线![]() 垂直于直线
垂直于直线![]() ;
;
(2)若搭边框共用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
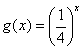
18. (本题满分14分,第1小题6分,第2小题8分)
已知函数![]() ,其中
,其中![]() ;
;
(1)依据![]() 的不同取值,讨论
的不同取值,讨论![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)已知![]() ,函数
,函数![]() 的反函数为
的反函数为![]() ,若函数
,若函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值
上的最大值
19. (本题满分14分,第1小题6分,第2小题8分)
已知椭圆![]() 的焦距为
的焦距为![]() ,且右焦点
,且右焦点![]() 与短轴的两个端点组成一个正三角形。若直线
与短轴的两个端点组成一个正三角形。若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() ,且在椭圆
,且在椭圆![]() 上存在点
上存在点![]() ,使得
,使得![]() (其中
(其中![]() 为坐标原点),则称直线
为坐标原点),则称直线![]() 具备性质
具备性质![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 垂直于
垂直于![]() 轴,且具备性质
轴,且具备性质![]() ,求直线
,求直线![]() 的方程
的方程
20. (本题满分16分,第1小题4分,第2小题6分,第3小题6分)
已知![]() ,函数
,函数![]() ;
;
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差低于1,求
上的最大值与最小值的差低于1,求![]() 的取值范围
的取值范围
21. (本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知函数![]() ,若存在常数
,若存在常数![]() ,对任意
,对任意![]() 都有
都有![]() ,则称函数
,则称函数![]() 为
为![]() 倍周期函数;
倍周期函数;
(1)判断![]() 是不是是
是不是是![]() 倍周期函数,说明理由;
倍周期函数,说明理由;
(2)证明![]() 是
是![]() 倍周期函数,且
倍周期函数,且![]() 的值是唯一的;
的值是唯一的;
(3)若![]() 是2倍周期函数,
是2倍周期函数,![]() ,
,![]() 表示
表示![]() 的前
的前![]() 项和,
项和,![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围
的取值范围
参考答案
1、![]()
2、1
3、2
4、![]()
5、![]()
6、-56
7、![]()
8、![]()
9、36
10、![]()
11、-2
12、![]()
13-16、CCAC
17、(1)证明略;(2)![]()
18、(1)当![]() 时,为偶函数,当
时,为偶函数,当![]() 时,为非奇非偶函数;(2)
时,为非奇非偶函数;(2)![]()
19、(1)![]() ;(2)
;(2)![]() 或
或![]()
20、(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]()
21、(1)不是;(2)![]() ;(3)
;(3)![]()







