文来中学初一数学周末“菜单式”作业（第九周）
1、填空题
1. 单项式
的次数是____________
2.“
与
的差的倒数”可用代数式表示为____________
3. 计算：
____________
4. 计算：____________
5. 假如分式
有意义，那样的取值范围是____________
6. 纳米是一种长度单位：
1纳米=米，已知某款手机油漆图层厚度为230纳米，那样该油漆图层厚度用科学计数法可表示为____________米
7. 若一个长方形的一条边长为
，面积为
，则该长方形的另一边长为____________
8. 计算：
____________
9. 若关于的二次三项式
是一个完全平方法，则m=____________
10. 方程
的解是____________
11. 若方程
有增根，则k=____________
12. A、B两地相距160千米，甲车和乙车的平均速度之比为4:5，两车同时从A地出发到B地，乙车比甲车早到30分钟，求甲车的平均速度。若设甲车平均速度为
千米/小时，则所列方程是____________
13. 若把一个边长为2厘米的等边
向右平移厘米，则平移后所得三角形的周长为____________厘米
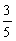14. 如图1，中，∠BAC=33°，将绕点A按顺时针方向旋转50°到 
，点B对应点
，点C对应点
，则
的度数为____________
15. 如图2，在正方形ABCD中，点E是AB边上的一点，AB=m，BE=n，将
绕着点C旋转，使CB与CD重合，这个时候点E落在点F处，联结EF，则
的面积可表示为____________（用含有m,n的代数式表示）
2、选择题
16. 下列计算正确的是（ ）
A. 
B. C. D. 
17. 下列算式中，结果为
的是（ ）
A. 
B. C. D. 
18. 已知甲、乙、丙均为的一次多项式，且其一次项的系数皆为正整数，若甲与乙相乘积为，乙与丙相乘为积
，则甲与丙相加的结果是（ ）
A. 
B. C. 
D. 
19. 如图3所示的五角星是旋转对称图形，该图形绕旋转对称中心O点按下列角度旋转后，能与其自己重
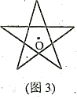合的是（ ）
A. 36° B. 108°
C. 180° D. 216°
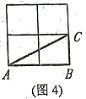20. 如图4，在2
2的正方形网格中，大家把顶点都在小正方形顶点上的三角形称为格点三角形，那样图中与成轴对称的格点三角形共有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
3、简答卷
21. 计算： 22. 计算：
23. 计算：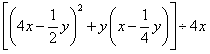
24. 分解因式：
25. 分解因式：
26. 解方程：
4、解答卷
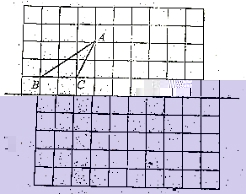
27. 如图5，方格纸中每一个小正方形的边长是一个单位长度，的顶点都是某个小正方形的顶点.
（1）将先向右平移5个单位，再向下平移2个单位，请画出平移后的
；
（2）将沿直线翻折，请画出翻折后的
.
28. 先化简：
，然后从
挑选一个适合的整数代入求值
29. 甲、乙两同学的家与学校的距离均为3000米，甲同学先步行600米，然后坐公交去学校、乙同学骑自行车去学校，已知甲步行速度是乙骑自车速的一半，公交车的速度是乙骑自车速的2倍，甲乙两人同时从家出发去学校，结果甲同学比乙同学早到2分钟.
（1）求乙骑自行车的速度；
（2）出发几分钟后，两人与学校的距离相等？
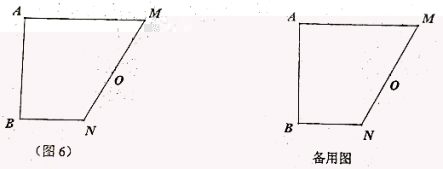
30. 如图6，已知四边形ABNM中，∠A=∠B=90°，点O为MN边的中点.
（1）请画出四边形ABNM关于点O的中心对称图形，且点A的对应点记为点C，点B的对应点记为点D；
（2）将四边形MNCD沿直线MN翻折，点C恰好与点A重合，点D的对应点记为E，请画出翻折后的图形，判断与面积之间的数目关系，并说明理由；
（3）对上述翻折后的图形，若四边形ANME与四边形ABNM重叠部分的面积是原四边形ABNM面积的，试求边BN与NC长度之间的数目关系.
