交大附中2018-2019学年第一学期摸底考试题
高中三年级数学
1、填空题
1.方程组![]() 的增广矩阵是___________.
的增广矩阵是___________.
2.若直线![]() 的参数方程为
的参数方程为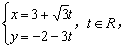 ,则直线
,则直线![]() 的倾斜角是_________.
的倾斜角是_________.
3.![]() _______.
_______.
4.已知数列![]() 的前
的前![]() 项的和
项的和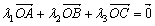 ,则当
,则当![]() 为正偶数时,
为正偶数时,![]() ______.
______.
5.函数![]() 是奇函数,那样
是奇函数,那样![]() ___________.
___________.
6.若函数![]() 无最值,则
无最值,则![]() 的取值范围是__________.
的取值范围是__________.
7.△ABC的内角A、B、C的对边分别为![]() ,已知△ABC的面积为
,已知△ABC的面积为![]() 则A=_______.
则A=_______.
8.设![]() ,
,![]() 是虚数单位,已知集合
是虚数单位,已知集合![]() ,若
,若
![]() ,则
,则![]() 的取值范围是__________.
的取值范围是__________.
9.双曲线![]() 的左焦点F引圆
的左焦点F引圆![]() 的切线,切点为T,延长F交双曲线右支于点P,若M是线段FP的中点,O为坐标原点,则
的切线,切点为T,延长F交双曲线右支于点P,若M是线段FP的中点,O为坐标原点,则![]() 的值是________.
的值是________.
10.胡涂涂同学用一颗均匀的骰子来概念递推数列![]() ,第一,他令
,第一,他令![]() ,当
,当![]() 时,他掷一次骰子,若所得点数大于
时,他掷一次骰子,若所得点数大于![]() ,即令
,即令![]() ,不然令
,不然令![]() ,则
,则![]() 的概率为_____
的概率为_____
.
11.关于![]() 的方程
的方程![]() 恰有3个实数根
恰有3个实数根![]() ,则
,则![]() _.
_.
12.由无理数理论引发的数字危机一直延续到19世纪,直到1872年,德国数学家戴德金从连续卖性的需要岀发,用有理数的“分割”来概念无理数,并把实数理论建
在严格的科学基础上,才结束了无理数被觉得“无理”的年代,也结束了持续2000多年的数学史上的首次大危机,所谓戴德金分割,是指或有理数集Q划分为两个非空的子集M与N,且满足![]() M中的每个元素都小于N中的每一素,则称
M中的每个元素都小于N中的每一素,则称![]() 为戴德金分割。试判断,对于任一戴德金分割
为戴德金分割。试判断,对于任一戴德金分割![]() ,下列选项中,可能成立的是________.
,下列选项中,可能成立的是________.
①M没最大元素,N有一个最小元素;
②M没最大元素,N也没最小元素;
③M有一个最大元素,N有一个最小元素;
④M有一个最大元素,N没最小元素
2、选择题
13.已知集合![]() ,则下列选项正确的是
,则下列选项正确的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.在空间直角坐标系![]() 中,若点P在第Ⅵ卦限,则与点P关于
中,若点P在第Ⅵ卦限,则与点P关于![]() 轴对称的点在
轴对称的点在
A.第Ⅰ卦限 B.第Ⅲ卦限 C.第V卦限 D.第Ⅶ卦限
15.设![]() 为实数,则“
为实数,则“![]() ”是“
”是“![]() 表示的曲线为双曲线”的
表示的曲线为双曲线”的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件
16.已知![]() 是同一平面上不共线的四点,若存在一组正实数
是同一平面上不共线的四点,若存在一组正实数![]() 使得
使得
![]() ,则三个角∠AOB、∠BOC、∠COA
,则三个角∠AOB、∠BOC、∠COA
A.都是钝角 B.至少有两个钝角
C.怡有两个钝角 D.至多有两个钝角
3、解答卷
17.
如图所示,三棱柱![]() 的侧面
的侧面![]() 是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点。
是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点。
若圆柱的轴截面是正方形,当点C是弧B的中点时,求异面直线![]() 与AB的所成角的大小;
与AB的所成角的大小;
当点C是弧AB的中点时,求四棱锥![]() 与圆柱的体积比.
与圆柱的体积比.

18.
已知![]() 是概念在R上的奇函数,求实数
是概念在R上的奇函数,求实数![]() 的值;
的值;
已知![]() 是概念在R上的函数,求实数
是概念在R上的函数,求实数![]() 的取值花围.
的取值花围.
19.
某工厂在生产商品时需要用到长度为698mm的d型和长度为518mm的B型两种钢管。工厂借助长度为4000mm的钢管原材料,剪裁成若干A型和B型光管,假设剪裁时损耗忽视不计,剪裁后所剩废料与原材料的百分比称为废料率。
要使剪裁的废料率小于45%,共有几种策略剪裁?请写出每种策略中分别被剪裁A型钢管和B型钢管的根数;
假设一根A型钢管和一根B型钢管能成为一套毛胚,假定只能按中的那些策略裁剪,若工厂需要生产320套毛胚,则至少需要采购多少根4000mm的钢管原材料?最后的废料率为多少?
20.
在平面上,给定非零向量![]() ,对任意向量
,对任意向量![]() ,概念
,概念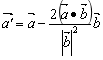
若![]() .b=,求
.b=,求![]() ;
;
若![]() ,证明:若地方向量
,证明:若地方向量![]() 的终点在直线
的终点在直线![]() 上,则地方向量
上,则地方向量![]() 的终点也在一条直线上;
的终点也在一条直线上;
已知存在单位向量![]() ,当地方向量
,当地方向量![]() 的终点在抛物线
的终点在抛物线![]() 上时,地方向量
上时,地方向量![]() 终点总在抛物线
终点总在抛物线![]() 上,曲线C和
上,曲线C和![]() 关于直线
关于直线![]() 对称,问直线
对称,问直线![]() 与向量
与向量![]() 满足什么关系?
满足什么关系?
21.求函数![]() 的分析式;
的分析式;
求证:![]() ;
;
求证:![]() .
.







