2019学年第一学期南模中学高二期末考试
数学学科
1、填空题（本大题共有12题，1~6题，每题4分，7~12题，每题5分，满分54分）
1．以原点为顶点，
轴为对称轴，并且经过
的抛物线的规范方程为______________．
2已知复数
满足
，则的虚部为____________________．
3．已知向
，
，
，则
____________________．
4双曲线
的一条渐近线的斜率是
，则
__________________．
5．设向量，
，若向量
与向量
共线，则___________________．
6．直线过点
，且在两条坐标轴上的截距互为相反数；则此直线的方程是_________________
7．已知是坐标原点，点
若点
为平面地区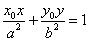
内的一个动点，则的取值范围为________________．
8已知动圆过定点
，且与圆
相切，则动圆的圆心
的轨迹方程是_________．
9．若直线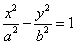
，（
为参数）与双曲线相交于
，
两点，则线段
的长为_____________．
10．过抛物线
的焦点作倾斜角为
的直线，与抛物线交于，两点（点在
轴左边则___________________．
11．将一圆的六个等分点分成两组相间的三点，它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星，如图所示的正六角星的中心为点，其中
，
y分别为点到两个顶点的向量；若将点到正六角星
个顶点的向量，都写成
的形式，则的最大值为_________________．
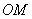
12．已知直角坐标平面上任意两点
、，概念
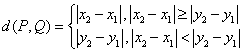为、两点的“很距离”．当平面上动点到定点的距离满足
时，则的取值范围是________________．
2、选择题（本大题共有4题，每题5分，满分20分）
13．设
，
为复数，则下列命题中肯定成立的是（ ）
A．假如
，那样
B．假如，那样
C．假如（
为正实数），那样
D．假如（为正实数），那样
14．在中，若，则是（ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D正三角形
15．设，分别为轴，轴上的两点，若以为直径的圆
与直线
相切，则圆的面积的最小值为（ ）
A．
B．
C．
D．
16．在平面直角坐标系
中，已知椭圆和
，为
上的动点，为上的动点，设
为
的最大值，记集合，则中元素的个数为（ ）
A无数个 B．个 C．个 D．
个
3、简答卷（本大题共有5题，满分76分）
17．复数
，
（1）若，求：（2）若在复平面内复数对应的点在第一象限，求的范围．
18．平面内有向量
，，，点为直线上的一个动点．
（1）当取最小值时，求
的坐标；
（2）当点满足（1）时，求
．
19．设
和是双曲线上的两点，线段
的中点为，直线不经过坐标原点．
（1）若直线和直线的斜率都存在且分别为
和
，求证：；
（2）若双曲线的焦点分别为、，点的坐标为，直线的斜率为
，求由四点、、、所围成四边形
的面积．
20．已知定点，动点在轴上运动，过点作直线交轴于点，延长至点，使
．点的轨迹是曲线．
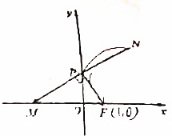
（1）求曲线的方程；
（2）若，是曲线上的两个动点，满足，证明：直线
过定点；
（3）若直线与曲线交于，两点，且，
，求直线的斜率
的取值范围．
21．教程曾有介绍：圆上的点处的切线方程为．大家将它结论推广：椭圆
上的点处的切线方程为，在解本题时可以直接应用．已知，直线，与椭圆有且只有一个公共点．
（1）求的值；
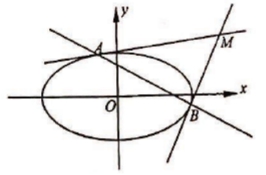
（2）设为坐标原点，过椭圆
上的两点、分别作该椭圆的两条切线、，且与交于点，当变化时，求
面积的最大值；
（3）在（2）的条件下，经过点作直线与该椭圆交于、两点，在线段上存在点，使
成立，试问：点是不是在直线上，请说明理由．
