课 题 | 高考考试数学复习专题——圆锥曲线 |
教学目的 | 1. 学会三种圆锥曲线的概念、图像和简单几何性质。 2. 准确理解基本定义（如直线的倾斜角、斜率、距离、截距等）。 3. 熟练学会基本公式（如两点间距离公式、点到直线的距离公式、斜率公式、定比分点的坐标公式、到角公式、夹角公式等）。 4. 熟练学会求直线方程的办法（如依据条件灵活使用各种形式、讨论斜率存在和没有的各种状况、截距是不是为0等等）。 5. 在解决直线与圆的地方关系问题中，要擅长运用圆的几何性质以降低运算。 6. 知道线性规划的意义及简单应用。 7. 熟知圆锥曲线中基本量的计算。 8． 学会与圆锥曲线有关的轨迹方程的求解办法（如：概念法、直接法、有关点法、参数法、交轨法、几何法、待定系数法等）。 9． 学会直线与圆锥曲线的地方关系的容易见到断定办法，能应用直线与圆锥曲线的地方关系解决一些容易见到问题。 |
重点难题 | 1. 学会与圆锥曲线有关的轨迹方程的求解办法。 2. 学会圆锥曲线中基本量的计算和直线与圆锥曲线的地方关系的容易见到断定办法。 |
圆锥曲线定义、办法、题型、易误点及应试方法总结
1.圆锥曲线的两个概念：
（1）______________________________：椭圆中，与两个定点F
，F
的距离的和等于常数
，且此常数必须要大于
，当常数等于时，轨迹是线段FF，当常数小于时，无轨迹；双曲线中，与两定点F，F的距离的差的绝对值等于常数，且此常数必须要小于|FF|，概念中的“绝对值”与＜|FF|不可忽略。若＝|FF|，则轨迹是以F，F为端点的两条射线，若﹥|FF|，则轨迹没有。若去掉概念中的绝对值则轨迹仅表示双曲线的一支。
__________已知定点
，在满足下列条件的平面上动点P的轨迹中是椭圆的是 A．
B．
C．
D．
（2）________________________________________“点点距为分子、点线距为分母”，其商即是离心率
。圆锥曲线的第二概念，给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系，要擅长运用第二概念对它们进行相互转化。
如已知点
及抛物线
上一动点P（x,y）,则y+|PQ|的最小值是_____
2.圆锥曲线的规范方程（标准方程是指中心（顶点）在原点，坐标轴为对称轴时的规范地方的方程）：
（1）椭圆：焦点在
轴上时（
）
（参数方程，其中
为参数），焦点在
轴上时
＝1（）。方程表示椭圆的充要条件是什么？（ABC≠0，且A，B，C同号，A≠B）。
如（1）已知方程
表示椭圆，则
的取值范围为____
（2）若
，且
，则
的最大值是____，
的最小值是___
（2）双曲线：焦点在轴上：
=1，焦点在轴上：
＝1（
）。方程表示双曲线的充要条件是什么？（ABC≠0，且A，B异号）。
如（1）双曲线的离心率等于
，且与椭圆有公共焦点，则该双曲线的方程_______
（2）设中心在坐标原点
，焦点
、
在坐标轴上，离心率
的双曲线C过点，则C的方程为_______
（3）抛物线：开口向右时
，开口向左时
，开口向上时
，开口向下时。
3.圆锥曲线焦点地方的判断（第一化成标准方程，然后再判断）：
（1）椭圆：由
,分母的大小决定，焦点在分母大的坐标轴上。
如已知方程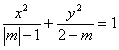
表示焦点在y轴上的椭圆，则m的取值范围是__
（2）双曲线：由,项系数的正负决定，焦点在系数为正的坐标轴上；
（3）抛物线：焦点在一次项的坐标轴上，一次项的符号决定开口方向。
特别提醒：（1）在求解椭圆、双曲线问题时，第一要判断焦点地方，焦点F，F的地方，是椭圆、双曲线的定位条件，它决定椭圆、双曲线标准方程的种类，而方程中的两个参数，确定椭圆、双曲线的形状和大小，是椭圆、双曲线的定形条件；在求解抛物线问题时，第一要判断开口方向；（2）在椭圆中，最大，
，在双曲线中，
最大，
。
