2019年普通高等学校招生全国统一考试
文科数学
本试题共5页。考试结束后，将本试题和答卷卡一并交回。
需要注意的地方：
1．答卷前，考生先将我们的名字、准考证号码填写了解，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题需要用2B铅笔填涂；非选择题需要用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹了解。
3．请根据题号顺序在答卷卡各题目的答卷地区内作答，超出答卷地区书写的答案无效；在草稿纸、试题上答卷无效。
4．作图可先用铅笔画出，确定后需要用黑色字迹的签字笔描黑。
5．维持卡面清洗，不要折叠，不要弄破、弄皱，不准用涂改液、修正带、刮纸刀。
1、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目需要的．
1．已知集合
，
，则A∩B=
A． B．
C． D．
2．设z=i，则
=
A．1+2i B．–1+2i
C．1–2i D．–1–2i
3．已知向量a=，b=，则|a–b|=
A． B．2
C．5 D．50
4．生物实验室有5只兔子，其中只有3只测量过某项指标，若从这5只兔子中随机取出3只，则恰有2只测量过该指标的概率为
A．
B．
C．
D．
5．在“一带一路”常识测验后，甲、乙、丙三人对成绩进行预测．
甲：我的成绩比乙高．
乙：丙的成绩比我和甲的都高．
丙：我的成绩比乙高．
成绩公布后，三人成绩互不相同且只有一个人预测正确，那样三人按成绩由高到低的次序为
A．甲、乙、丙 B．乙、甲、丙
C．丙、乙、甲 D．甲、丙、乙
6．设f为奇函数，且当x≥0时，f=
，则当x<0时，f=
A．
B．
C．
D．
7．设α，β为两个平面，则α∥β的充要条件是
A．α内有无数条直线与β平行
B．α内有两条相交直线与β平行
C．α，β平行于同一条直线
D．α，β垂直于同一平面
8．若x1=
，x2=
是函数f=两个相邻的极值点，则
=
A．2 B．
C．1 D．
9．若抛物线y2=2px（p>0）的焦点是椭圆
的一个焦点，则p=
A．2 B．3
C．4 D．8
10．曲线y=2sinx+cosplayx在点处的切线方程为
A．
B．
C．
D．
11．已知a∈（0，
），2sin2α=cosplay2α+1，则sinα=
A．
B．
C．
D．
12．设F为双曲线C：
（a>0，b>0）的右焦点，O为坐标原点，以OF为直径的圆与圆x2+y2=a2交于P、Q两点．若|PQ|=|OF|，则C的离心率为
A． B．
C．2 D．
2、填空题：本题共4小题，每小题5分，共20分．
13．若变量x，y满足约束条件
则z=3x–y的最大值是___________.
14．国内高铁飞速发展，技术先进．经统计，在经停某站的高铁列车中，有10个车次的正点率为0.97，有20个车次的正点率为0.98，有10个车次的正点率为0.99，则经停该站高铁列车所有车次的平均正点率的估计值为___________.
15．的内角A，B，C的对边分别为a，b，c.已知bsinA+acosplayB=0，则B=___________.
16．中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．（本题第一空2分，第二空3分．）
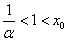
3、解答卷：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考试试题，每一个考试试题考生都需要作答．第22、23题为选考试试题，考生依据需要作答．
（一）必考试试题：共60分。
17．（12分）
如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.
（1）证明：BE⊥平面EB1C1；
（2）若AE=A1E，AB=3，求四棱锥的体积．
18．（12分）
已知
是各项均为正数的等比数列，.
（1）求的通项公式；
（2）设
，求数列的前n项和.
19．（12分）
某行业主管部门为知道本行业中小微型企业的生产状况，随机调查了100个企业，得到这类企业首季相对于前一年首季产值增长率y的频数分布表.
|
|
|
|
|
|
企业数 | 2 | 24 | 53 | 14 | 7 |
的分组 （1）分别估计这种企业中产值增长率高于40%的企业比率、产值负增长的企业比率；
（2）求这种企业产值增长率的平均数与标准差的估计值（同一组中的数据用该组区间的中点值为代表）.（精准到0.01）
附：.
20．（12分）
已知
是椭圆的两个焦点，P为C上一点，O为坐标原点．
（1）若
为等边三角形，求C的离心率；
（2)假如存在点P，使得
，且
的面积等于16，求b的值和a的取值范围.
21.（12分）
已知函数
.证明：
（1）
存在唯一的极值点；
（2）有且仅有两个实根，且两个实根互为倒数.
（二）选考试试题：共10分．请考生在第22、23题中任选一题作答。假如多做，则按所做的第一题计分．
22．[选修4-4：坐标系与参数方程]（10分）
在极坐标系中，O为极点，点
在曲线
上，直线l过点
且与
垂直，垂足为P.
（1）当时，求
及l的极坐标方程；
（2）当M在C上运动且P在线段OM上时，求P点轨迹的极坐标方程.
23．[选修4-5：不等式选讲]（10分）
已知
（1）当
时，求不等式
的解集；
（2）若时，，求的取值范围.
1．C 2．D 3．A 4．B 5．A 6．D
7．B 8．A 9．D 10．C 11．B 12．A
13．9 14．0.98 15． 16．
17．解：（1）由已知得B1C1⊥平面ABB1A1，BE
平面ABB1A1，
故.
又
，所以BE⊥平面
.
（2）由（1）知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E，所以
，故AE=AB=3，.
作
，垂足为F，则EF⊥平面，且
.
所以，四棱锥的体积.
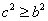
18．解：（1）设
的公比为q，由题设得
，即
.
解得（舍去）或q=4.
因此的通项公式为.
（2）由（1）得，因此数列的前n项和为
.
19.解：（1）依据产值增长率频数分布表得，所调查的100个企业中产值增长率高于40%的企业频率为.
产值负增长的企业频率为
.
用样本频率分布估计总体分布得这种企业中产值增长率高于40%的企业比率为21%，产值负增长的企业比率为2%.
（2）
，
，
，
所以，这种企业产值增长率的平均数与标准差的估计值分别为30%，17%.
20.解：（1）连结，由为等边三角形可知在中，，
，，于是，故的离心率是.
（2）由题意可知，满足条件的点
存在当且仅当，，
，即，①
，②
，③
由②③及得，又由①知
，故
.
由②③得
，所以，从而
故
.
当，时，存在满足条件的点P.
所以，的取值范围为
.
21.解：（1）的概念域为（0，+）.
.
由于单调递增，单调递减，所以
单调递增，又
，
，故存在唯一
，使得.
又当时，，单调递减；当时，
，单调递增.
因此，存在唯一的极值点.
（2）由（1）知，又，所以
在内存在唯一根.
由得.
又，故是在的唯一根.
综上，有且仅有两个实根，且两个实根互为倒数.
22．解：（1）由于在C上，当时，.
由已知得.
设为l上除P的任意一点.在
中，
经检验，点在曲线上.
所以，l的极坐标方程为.
（2）设，在
中， 即
..
由于P在线段OM上，且，故的取值范围是
.
所以，P点轨迹的极坐标方程为 .
23．解：（1）当a=1时，.
当时，
；当时，.
所以，不等式的解集为.
（2）由于，所以.
当，时，.
所以，的取值范围是.
