上海行知中学高二第二学期首次月考数学试题
考试时间：
120 分钟 满分：
150 分
1、填空题（1-6 题每题 4 分，7-12 题每题 5 分，共 54 分）
1、已知点 A ， B ，且
= 
,则点 D 的坐标是____________________；
答案：
2、将参数方程
（q 为参数）化为普通方程，所得方程是____________________；
答案： 2 + y 2 = 4
3、已知圆锥的母线与底面所成角为 45°，则圆锥的侧面积与底面积的比值为____________________；
答案：
4、已知双曲线
，则以双曲线的焦点为顶点，以双曲线顶点为焦点的椭圆方程
为____________________；
答案：
5、一个与球心距离为
的平面截球所得的圆的面积为 p ，该截面圆周上有两点 A、B ，且| AB |= 2 ，则 A、B 两点
的球面距离为____________________；
答案：
6 、已知正四棱锥的底面积为 4cm2 ，体积为 4cm3 ，设它侧面上的斜高与底面所成角大小为 q ，则 sin q 的值
是____________________；
答案：
7、已知 2 + ai ，b + i（其中 a, b Î R ）是实系数一元二次方程 x2 + px + q = 0 的两个根，则的值为__________;
答案：
8、圆柱的轴截面是边长为 5cm 的正方形 ABCD ，一只蚂蚁沿着圆柱的侧面从点 A 爬到点 C ，爬过的最短路程长度
是____________________cm ；
答案：
9、已知△ABC 的面积为 1，在△ABC 所在平面内有两点 P 、Q ，满足
则四边形
BCPQ 的面积为____________________；
答案：
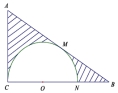10、如图， △ABC 中， ÐACB = 90° , ÐABC = 30° , BC =，在三角形内挖去一个半圆（圆
心 O 在边 BC 上，半圆与 AC 、AB 分别相切于点 C 、M ，与 BC 交于点 N ），将它绕直线 BC
旋转一周得到一个旋转体，则该旋转体体积为____________________；
答案：
11、对 n Î N ，设抛物线 y 2= 2 x ，过 P 任作直线 l 与抛物线交与 A n， B n两点，则数列
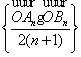的前 n 项和为____________________；
答案： -n2 - n
12、在 xOy 平面上，将两个半圆弧 2 + y 2 = 1 和 2 + y 2 = 1 ，两条
直线 y = 1 和 y = -1 围成的封闭图形记为 D ，如图中阴影部分。记 D 绕 y 轴旋转一周而成
的几何体为 W ，过 作 W 的水平截面，所得截面面积为 4p
+ 8p ，试
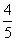用祖暅原理，一个平放的圆柱和一个长方体，得出 W 的体积值为____________________；
答案： 2p 2 + 16p
2、选择题（每题 5 分，共 20 分）
13、已知直线 a 、 b 都在平面a 外，以下假命题的是（ ）
A、 a∥b ， b∥a ，则 a∥a B、 a⊥b ， b⊥a ，则 a∥a
C、 a∥a ， b∥a ，则 a∥b D、 a⊥a ， b⊥a ，则 a∥b
答案：C
14、在△ABC ，有命题①若
× > 0 ,则△ABC 为锐角三角形；② + 
+ 
= 0 ；
③ × = 0 ,则△ABC 为等腰三角形；④- = ，
以上命题正确的是（ ）
A、①② B、①④ C、②③ D、②③④
答案：C
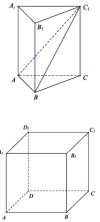
15、如图，在正三棱柱 ABC - A1 B1C1 中，AB = 1 ，若二面角 C - AB - C1 的大小为 60°，则点 C 到
平面 ABC1 的距离为（ ）
A、
B、 C、
D、
答案：A
16、正方体 ABCD - A1 B1C1 D1 的棱长为 a ，平面 ABCD 上一动点 M 到直线 AD 的距离与到直线
D1C1 的距离相等，则点 M 的轨迹为（ ）
A、直线 B、椭圆 C、抛物线 D、双曲线
答案：D
3、解答卷（17-19 题⇿题 14 分，20 题 16 分，21 题 18 分，共 76 分）
17、（本题 2 小题，第 1 小题 6 分，第 2 小题 8 分，满分 14 分）
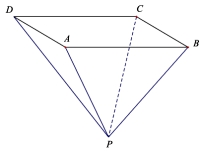
如图已知四棱锥 P - ABCD 的底面是边长为 6 的正方形，侧棱 PA 的长为 8，且垂直于底面，点 M 、 N 分别是 DC 、
AB 的中点。
求：（1）异面直线 PM 与 CN 所成角的正切值；
（2）四棱锥 P - ABCD 的表面积.
答案：
（1）
（2）144
18、（本题 2 小题，第 1 小题 6 分，第 2 小题 8 分，满分 14 分）
已知复数 z = a + bi ，其中 a 、b 为实数，i 为虚数单位， 
为 z 的共轭复数，且存在非零实数 t ，使
成立.
（1）求 2a + b 的值；
（2）若| z - 2 |£ 5 ，求实数 a 的取值范围.
答案：（1）6；（2）
19、（本题 2 小题，第 1 小题 6 分，第 2 小题 8 分，满分 14 分）
用一块钢锭浇铸一个厚度均匀，且全方位积为 2 平米的正四棱锥形有盖容器（如图），设容器高为 h 米，盖子边长 为 a 米.
（1）求 a 关于 h 的函数分析式；
（2）设容器的容积为V 立方米，则当 h 为什么值时，V 最大，求出V 的最大值.（求解本题时，不计容器的厚度） 答案：
（1） a =
；
（2） h = 1 米时，V 有最大值，V 的最大值为平米。
20、（本题 3 小题，第 1 小题 4 分，第 2 小题 4 分，第 3 小题 8 分，满分 16 分）
如图，在正三棱柱 ABC - A1 B1C1 中， AB = 3 ， AA1 = 4 ， M 为 AA1 的中点， P 是 BC 上一
点，且由 P 沿棱柱侧面经过棱 CC1 到 M 点的最短路线长为
，设这条最短路线与 CC1 的
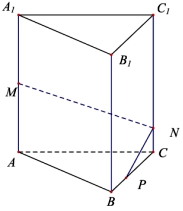交点为 N 。求：
（1）该三棱柱的侧面展开图的对角线长；
（2） PC 和 NC 的长；
（3）平面 NMP 和平面 ABC 所成锐二面角大小的正切值.
答案：
（1）
；（2） PC = 2 ， NC = ；（3）
21、（本题 3 小题，第 1 小题 4 分，第 2 小题 6 分，第 3 小题 8 分，满分 18 分）
给定椭圆 C : 
，称圆心在原点，半径为
的圆是椭圆 C 的“随着圆”.若椭圆 C 的一个
焦点为 F1 ，其短轴上的一个端点到 F1 的距离为
（1）求椭圆 C 的方程及其“随着圆”方程；
（2）若倾斜角 45°的直线 l 与椭圆 C 只有一个公共点，且与椭圆 C 的随着圆相交于 M 、N 两点，求弦 MN 的的长；
（3）点 P 是椭圆 C 的随着圆上一个动点，过点 P 作直线 l1 、 l2 ，使得 l1 、 l2 与椭圆 C 都只有一个公共点，判断 l1 、
l2 的地方关系，并说明理由.
答案：
（1）椭圆方程：；随着圆方程： x2 + y2 = 1 ；
（2） 2
（3）垂直，（斜率乘积为 -1 ，分斜率存在与否）
