初三 数学综合测试
（满分 120 分，考试时间 100 分钟）
1、选择题（每小题 3 分，共 30 分）
 |
 |
 |
 |
1. 下列图案中，既是中心对称又是轴对称图形的个数有（ ）
A．1 个 | B．2 个 | C．3 个 | D．4 个 |
2. 方程 x2=4x 的根是（ A．x=4 | ） |
B．x=0 |
|
C．x1=0，x2=-4 |
| D．x1=0，x2=4 |
|
3. 如图，点 A，B，C 在⊙O 上，∠C=44°，则∠AOB 的大小为（ ）
A．22° B．88° C．66° D．70°
 |
4. 下列说法中，正确的是（ ）
A．随机事件发生的概率为 1
2
B．不可能事件发生的概率为 0
C．概率非常小的事件不可能发生
D．投掷一枚硬币 100 次，正面朝上的次数必为 50 次
5. 可将抛物线 y=x2-4（ ）单位，得到 y=x2．
A．向上平移 4 个 B．向下平移 4 个
C．向右平移 4 个 D．向左平移 4 个
a2 +1 1 1
6. 若函数 y = - 的图象上有三个点，，，则 y1，
x 2 2
y2，y3 的大小关系是（ ）
A．y1＜y2＜y3 B．y3＜y2＜y1 C．y3＜y1＜y2 D．y2＜y1＜y3
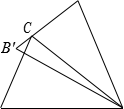
7. 如图，将△ABC 绕点 A 顺时针旋转肯定的角度至△AB′C′处，使得点 C 恰好在线 B′C′上，若∠ACB=75°，则∠BCB′的度数为（ ）
A．20° B．25° C．30° D．35°
C'
B A
8. 抛物线 y=ax2+bx+c（a≠0）的部分图象如图所示，与 x 轴的一个交点坐标为
，抛物线的对称轴 x=1．下列结论中：①abc＞0；②2a+b=0；③方程
ax2+bx+c=3 有两个不相等的实数根；④抛物线与 x 轴的另一个交点坐标为；⑤若点 A在该抛物线上，则 am2+bm+c≤a+b+c．其中正确的有 （ ）
A．5 个 B．4 个 C．3 个 D．2 个
 |
9. 如图，正方形 ABCO 和正方形 CDEF 的顶点 B，E 在双曲线 y = 4（x＞0）上，
x
连接 OB，OE，BE，则 S△OBE 的值为（ ）
A．2 B．2.5 C．3 D．3.5
 |
10. 如图，在平面直角坐标系中，边长为 1 的正方形 OA1B1C1 的两边在坐标轴上， 以它的对角线 OB1 为边作正方形 OB1B2C2，再以正方形 OB1B2C2 的对角线
OB2 为边作正方形 OB2B3C3，以此类推，……，则正方形 OB2 015B2 016C2 016
的顶点 B2 016 的坐标是（ ）
A．2015 ， -2015 )
B．2015 ， 2015 )
C．
D．
2、填空题（每小题 3 分，共 15 分）
11. 已知抛物线 y=ax2+bx+c（a≠0）与 x 轴交于 A，B 两点，若点 A 的坐标为，抛物线的对称轴为直线 x=2，则线段 AB 的长为____________________．
12.
 |
如图，在平面直角坐标系 xOy 中，△AOB 可以看作是△OCD 经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△OCD 得到△AOB 的过程：____________________．
13. 在不透明的口袋中有若干个完全一样的红色小球，现放入 10 个仅颜色不同
的白色小球，均匀混合后，有放回的随机摸取 30 次，有 10 次摸到白色小球， 据此估计该口袋中原有红色小球个数为____________________．
14. 如图，菱形 OABC 中，∠A=120°，OA=1，将菱形 OABC 绕点 O 按顺时针方向旋转 90°至菱形 OA′B′C′，则图中阴影部分的面积是____________________．
B B'
C A'
A C'
O
15. 如图，已知∠MON=120°，点 A，B 分别在 OM，ON 上，且 OA=OB=a，将射线 OM 绕点 O 逆时针旋转得到 OM′，旋转角为 α（0°＜α＜120°且 α≠60°），作点 A 关于直线 OM′的对称点 C，画直线 BC 交 OM′于点 D，连接 AC，AD， 有下列结论：
①AD=CD；
②∠ACD 的大小伴随 α 的变化而变化；
③当 α=30°时，四边形 OADC 为菱形；
④△ACD 面积的最大值为
3a2 ．
其中正确的是____________________（把你觉得正确结论的序号都填上）．
N M′
C
B D
α M
O A
3、解答卷（本大题共 8 个小题，满分 75 分）
16. （8 分）已知关于 x 的一元二次方程 x2-2x+k=0．
（1）若方程有实数根，求 k 的取值范围；
（2）在（1）的条件下，假如 k 是满足条件的最大的整数，且方程 x2-2x+k=0 一根的相反数是一元二次方程x2-3mx-7=0 的一个根，求 m 的值及这个方程的另一根．
17. （9 分）在一次数学兴趣小组活动中，李燕和刘凯两位同学设计了如图所示的两个转盘做游戏（每一个转盘被分成面积相等的几个扇形，并在每一个扇形地区内标上数字）．游戏规则如下：两人分别同时转动甲、乙转盘，转盘停止后，若指针所指地区内两数和小于 12，则李燕获胜；若指针所指地区内两数和等于 12，则为平局；若指针所指地区内两数和大于 12，则刘凯获胜（若指针停在等分线上，重转一次，直到指针指向某一份内为止）．
（1）请用列表或画树状图的办法表示出上述游戏中两数和的所大概的结果；
（2）分别求出李燕和刘凯获胜的概率．
| |
 |
甲 乙
18. （9 分）如图，在平面直角坐标系中，直线 y = - 1 x 反比率函数 y = k （k≠0）
2 x
在第二象限内的图象相交于 A．
（1）求反比率函数的分析式；
（2）将直线 y = - 1 x 向上平移后与反比率函数图象在第二象限内交于点 B，
2
与 y 轴交于点 C，且△ABO 的面积为 3 ，求直线 BC 的分析式．
2
| |
19. （9 分）如图，在△ABC 中，∠C=90°，点 O 在 AC 上，以 OA 为半径的⊙O 交 AB 于点 D，BD 的垂直平分线交 BC 于点 E，交 BD 于点 F，连接 DE．
（1）判断直线 DE 与⊙O 的地方关系，并说明理由；
（2）若 AC=6，BC=8，OA=2，求线段 DE 的长．
C
A D F B
20. （9 分）小明依据学习函数的经验，对函数 y = x + 1 的图象与性质进行了探
x
究．
下面是小明的探究过程，请补充完整：
（1）函数 y = x + 1 的自变量 x 的取值范围是 ；
x
（2）下表列出了 y 与 x 的几组对应值，请写出 m，n 的值：m=____________________，
n=____________________；
x | … | －3 | －2 | －1 | - 1 2 | - 1 3 | 1
3 | 1
2 | 1 | 2 | 3 | 4 | … |
y | … | - 10 3 | - 5 2 | －2 | - 5 2 | - 10 3 | m | 5
2 | 2 | 5
2 | n | 17
4 | … |
（3）如图，在平面直角坐标系 xOy 中，描出了以上表中各对对应值为坐标的点，依据描出的点，画出该函数的图象；
（4）结合函数的图象，请完成：
①当 y = - 17 时，x= ；
4
②写出该函数的一条性质____________________；
③若方程 x + 1 = t 有两个不相等的实数根，则 t 的取值范围是 ．
x
 |
21. （10 分）伴随大家生活质量的提升，短途旅游日趋热门，我市某旅游社推出了“省内景点1日游”项目，团队人均报名成本 y（元）与团队报名人数 x
（人）之间的函数关系如图所示，旅游社规定团队人均报名成本不可以低于 88
元，旅游社收到的团队总报名成本为 w（元）．
（1）直接写出当 x≥20 时，y 与 x 之间的函数关系式及自变量 x 的取值范围；
（2）六一当天旅游社收到某个团队的总报名费为 3 000 元，报名旅游的人数是多少？
（3）当一个团队有多少人报名时，旅游社收到的总报名费最多？最多总报名费是多少元？
120
96
O 20 32 x（人）
22. （10 分）（1）【操作发现】
如图 1，将△ABC 绕点 A 顺时针旋转 60°，得到△ADE，连接 BD，则
∠ABD=____________________度．
（2）【类比探究】
如图 2，在等边三角形 ABC 内任取一点 P，连接 PA，PB，PC，求证：以 PA，
PB，PC 的长为三边必能组成三角形．
（3）【解决问题】
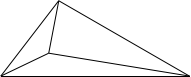
如图 3，在边长为 的等边三角形 ABC 内有一点 P，∠APC=90°，∠BPC=
120°，求△APC 的面积．
（4）【拓展应用】
如图 4 是 A，B，C 三个村子地方的平面图，经测量 AC=4，BC=5，∠ACB=30°，
P 为△ABC 内的一个动点，连接 PA，PB，PC．求 PA+PB+PC 的最小值．
A
A
B C
图2
A
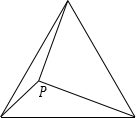
B C
图3
A
P
B C
图4
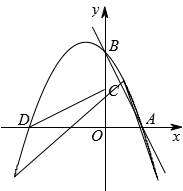
（11 分）如图 1，直线 l：y=mx+n（m＜0，n＞0）与 x，y 轴分别相交于 A，
B 两点，将△AOB 绕点 O 逆时针旋转 90°得到△COD，过点 A，B，D 的抛物线 C0 叫做 l 的关联抛物线，而 l 叫做 C0 的关联直线．
（1）若 l：y=-2x+2，则 C0 表示的函数分析式为______________________________；若 C0：y=-x2-3x+4，则 l 表示的函数分析式为____________________．
（2）C0 的对称轴为____________________（用含 m，n 的代数式表示）．
（3）如图 2，若 l：y=-2x+4，C0 的对称轴与 CD 相交于点 E，点 F 在 l 上， 点 Q 在 C0 的对称轴上．当以点 C，E，Q，F 为顶点的四边形是以 CE 为一边的平行四边形时，求点 Q 的坐标．
（4）如图 3，若 l：y=mx-4m，G 为 AB 中点，H 为 CD 中点，连接 GH，M
为 GH 中点，连接 OM．若OM = ，直接写出 l，C0 表示的函数分析式．
 |
 |
图 1 图 2 图 3
