__________
专题 06一次函数的应用问题
__________
【考试知识点1】行程问题
【例1】（2019·浙江中考考试真题）某校的甲、乙两位老师同住一小区，该小区与学校相距2400米. 甲从小区步行去学校，出发10分钟后乙再出发，乙从小区先骑公共自行车，途经学校义骑行若干米到达还车点后，立即步行走回学校. 已知甲步行的速度比乙步行的速度每分钟快5米. 设甲步行的时间为
，图1中线段
和折线
分别表示甲、乙离开小区的路程
与甲步行时间的函数关系的图象；图2表示甲、乙两人之间的距离
与甲步行时间的函数关系的图象.依据图1和图2中所给信息，解答下列问题：
求甲步行的速度和乙出发时甲离开小区的路程；
求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离；
在图2中，画出当
时关于的函数的大致图象.
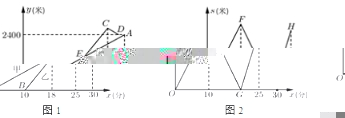
【答案】甲步行的速度是80 米/分，乙出发时甲离开小区的路程是800 米；乙到达还车点时，甲、乙两人之间的距离是700 米；图象如图所示见分析.
【分析】（1）依据函数图象中的数据可以求得甲步行的速度和乙出发时甲离开小区的路程；
（2）依据函数图象中的数据可以求得OA的函数分析式，然后将x=18代入OA的函数分析式，即可求得点E的纵坐标，进而可以求得乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离；
（3）依据题意可以求得乙到达学校的时间，从而可以函数图象补充完整．
【解析】
由题意，得：甲步行的速度是 ，
∴乙出发时甲离开小区的路程是
.
设直线的分析式为:
，
∵直线过点
，
∴
，
解得
，
∴直线的分析式为:
.
∴当时，
，
∴乙骑自行车的速度是
.
∵乙骑自行车的时间为
，
∴乙骑自行车的路程为
.
当
时，甲走过的路程是 ，
∴乙到达还车点时，甲、乙两人之间的距离是
.
乙步行的速度为：80-5=75（米/分），
乙到达学校用的时间为：25+（2700-2400）÷75=29（分），
当25≤x≤30时s关于x的函数的大致图象如图所示．
【点睛】本题考查一次函数的应用，解答本题的重点是明确题意，借助一次函数的性质和数形结合的思想解答．
【变式1-1】（2019·山东中考考试真题）小王骑车从甲地到乙地，小李骑车从乙地到甲地，小王的速度小于小李的速度，两人同时出发，沿同一条公路匀速前进．图中的折线表示两人之间的距离
与小王的行驶时间
之间的函数关系．
请你依据图象进行探究：
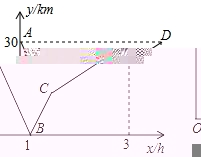
（1）小王和小李的速度分别是多少？
（2）求线段
所表示的与之间的函数分析式，并写源于变量的取值范围．
【答案】（1）小王和小李的速度分别是
、
；（2）．
【分析】
依据题意和函数图象中的数据可以分别求得王和小李的速度；
依据中的结果和图象中的数据可以求得点C的坐标，从而可以解答本题．
【解析】
解：（1）由图可得，
小王的速度为：，
小李的速度为：
，
答：小王和小李的速度分别是、；
（2）小李从乙地到甲地用的时间为：
，
当小李到达甲地时，两人之间的距离为：
，
∴点的坐标为，
设线段所表示的与之间的函数分析式为
，
，解得，
即线段所表示的与之间的函数分析式是．
【点睛】本题考查一次函数的应用，解答本题的重点是明确坐标轴中xy所表示的对象量，借助一次函数的性质和数形结合的思想解答．
【变式1-2】（2019·江苏中考考试真题）“低碳生活，绿色出行”是一种环保，健康的生活方法，小丽从甲地出发沿一条笔直的公路骑车前往乙地，她与乙地之间的距离y与出发时间之间的函数关系式如图1中线段AB所示，在小丽出发的同时，小明从乙地沿同一条公路骑车匀速前往甲地，两人之间的距离S与出发时间x之间的函数关系式如图2中折线段CD-DE-EF所示.
（1）小丽和小明骑车的速度各是多少？
（2）求E点坐标，并讲解点的实质意义.
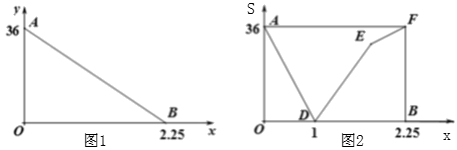
【答案】（1），
；（2）E
.
【分析】察看图1可知小丽骑行36千米用了2.25小时，依据速度=路程÷时间可求出小丽的速度，察看图2可知小丽与小明1小机会遇，由此即可求得小明的速度；
察看图2，结合两人的速度可知点E为小明到达甲地，依据有关数据求出坐标即可.
【解析】
V小丽=36÷2.25=16，
V小明=36÷1-16=20；
36÷20=，
16×=
，
所以点E的坐标为，
实质意义是小明到达了甲地.
【点睛】本题考查了一次函数的应用——行程问题，弄清题意，正确剖析图象，得出有用的信息是解题的重点.
