2020年人教部编版初一下册数学期末模拟试题
题号 | 一 | 二 | 三 | 总分 |
得分 |
|
|
|
|
1、选择题
1.在下面的问题中,不合适全方位调查的是
A.知道你们班同学的身高状况 B.知道我校教师的年龄状况
C.知道某单位所有家庭的年收入状况 D.知道某区域中小学生的视力状况
2.下列各等式中,正确的是
A.-=-3 B.±=3 C.2=-3 D.=±3
3.如图,AB∥CD,∠C=70°,BE⊥BC,则∠ABE等于
A.20° B.30° C.35° D.60°

![]()

4.已知a,b两个实数在数轴上的对应点如图所示,则下列各式肯定成立的是
A.a-1>b-1 B.3a>3b C.-a>-b D.a+b>a-b
5.假如点M是第二象限的点,则a的取值范围在数轴上表示正确的是
![]()
6.如图,将四边形ABCD先向左平移3个单位长度,再向下平移3个单位长度,那样点D的对应点D′的坐标是
A. B. C. D.
7.小颖家离学校1 200米,其中有一段为上坡路,另一段为下坡路,她去学校共用了16分钟,假设小颖上坡时的平均速度是3千米/时,下坡时的平均速度是5千米/时,若设小颖上坡用了x分钟,下坡用了y分钟,依据题意可列方程组为
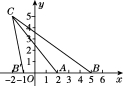
A.x+y=16 B.x+y=16 C.x+y=16 D.x+y=16
8.若关于x的不等式组>x+a有四个整数解,则a的取值范围是
A.-4≤-2 B.-4≤a<-2 C.-4≤a≤-2 D.-4-2
9.阅读对人成长的影响是巨大的,一本好书总是能改变人的一生.如图是某校三个年级学生人数分布的扇形统计图,其中初二学生人数为408人,下表是该校学生阅读课外书本状况统计表.依据图表中的信息,可知该校学生平均每个人读课外书的本数是
图书类型 | 频数 | 频率 |
科普常识 | 840 | B |
名人传记 | 816 | 0.34 |
漫画丛记 | A | 0.25 |
其他 | 144 | 0.06 |
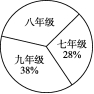
A.2本 B.3本 C.4本 D.5本
10.已知方程组x-y=3a+5的解x为正数,y为非负数,给出下列结论:①-1<a≤1;②当a=-3时,x=y;③当a=-2时,方程组的解也是方程x+y=5+a的解.其中正确的是
A.①② B.②③ C.①③ D.①②③
2、填空题
11.实数7,,-8,3,,3中的无理数是__________________.
12.下列命题:①不相交的直线是平行线;②同位角相等;③假如两个实数的平方相等,那样这两个实数也相等;④对顶角相等.其中真命题的序号是________.
13.已知点P在第二象限,点P到x轴的距离是2,到y轴的距离是3,那样点P的坐标是________.
14.在全国初中数学竞赛中,都匀市有40名同学进入复赛,把他们的成绩分为六组,第一组~第四组的人数分别为10,5,7,6,第五组的频率是0.2,则第六组的频率是________.
15.如图,直线AB,CD交于点O,OE⊥AB,若∠AOD=50°,则∠COE的度数为________.



16.如图,点E在AC的延长线上,给出的四个条件:∠3=∠4;∠1=∠2;∠A=∠DCE;∠D+∠ABD=180°.能判断AB∥CD的有________个.
17.如图,ABCD是一块长方形场地,AB=18米,AD=11米,从A,B两处入口的小路的宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为________平米.
18.假如关于x,y的方程组2x-y=9-2k的解满足3x+y=5,则k的值为________.
19.有10名菜农,每个人可种甲种蔬菜3亩或乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,若要使总收入高于15.6万元,则至多安排________人种甲种蔬菜.
20.公元3世纪,国内古时候数学家刘徽就能借助近似公式≈a+2a得到的近似值.他的算法是先将看成,由近似公式得到≈1+2×1=2;再将看成4,由近似公式得到≈2+2=12;…依此算法,所得的近似值会愈加精准.当获得近似值408时,近似公式中的a是________,r是________.
3、解答卷
21.计算下列各题:
+-27-;-8-+2+|1-|.
22.解方程组或不等式组:
3x+2y=13;② +1.②
23.在平面直角坐标系中,三角形ABC的边AB在x轴上,且AB=3,顶点A的坐标为,顶点C的坐标为.
画出所有符合条件的三角形ABC,并写出点B的坐标;
求△ABC的面积.
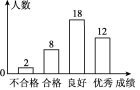
24.某学校为知道初一男孩体质健康状况,随机抽取若干名男孩进行测试,测试结果分为出色、好、合格、不合格四个等级,统计整理数据并绘制图①、图②两幅不完整的统计图,请依据图中信息回答下列问题:
本次同意随机抽样调查的男孩人数为________人,扇形统计图中“好”所对应的圆心角的度数为________;
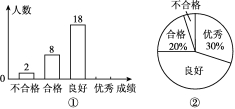
补全条形统计图中“出色”的空缺部分;
若该校初一共有男孩480人,请估计全年级男孩体质健康情况达到“好”的人数.
25.如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠下载成本=∠3,
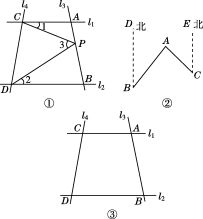
点P在线段AB上.
若∠1=22°,∠2=33°,则∠3=________;
试找出∠1,∠2,∠3之间的等量关系,并说明理由;
应用中的结论解答下列问题;
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
假如点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系,直接写出结论即可.
26.今年夏季,我州某区域遭受罕见的水灾,“水灾无情人有情”,凯里某单位给该区域某中学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
求饮用水和蔬菜各有多少件.
现计划租用甲、乙两种型号的货车共8辆,一次性将这批饮用水和蔬菜全部运往受灾区域某中学.已知每辆甲型货车最多可装饮用水40件和蔬菜10件,每辆乙型货车最多可装饮用水和蔬菜各20件,则凯里某单位安排甲、乙两种货车时有几种策略?请你帮助设计出来.
在的条件下,假如甲型货车每辆需付运费400元,乙型货车每辆需付运费360元.凯里某单位应选择哪种策略可使运费最少?最少运费是多少元?
答案
1、1.D2.A3.A
4.C点拨:由数轴可知a<b<0,依据不等式的性质可知a-1<b-1,3a<3b,-a>-b,a+b<a-b,故C正确.
5.A点拨:由于点M在第二象限,所以1+a>0.解不等式组得-1<a<3.故选A.
6.D点拨:由题图可知D点的坐标为,向左平移3个单位长度,再向下平移3个单位长度,即横坐标减3,纵坐标减3,即D′,故选D.
7.B
8.B点拨:先解不等式组,得8 则这四个整数解为9,10,11,12.从图中可知12<2-4a<13.即-4- 9.A 10.B点拨:解方程组得y=-2a-2. ①由题意得,3+a>0,-2a-2≥0, 解得-3<a≤-1,①不正确; ②当3+a=-2a-2时,a=-3,②正确; ③当a=-2时,x+y=1-a=3,5+a=3,③正确. 故选B. 2、11.,3,3 12.④13. 14.0.115.40°16.3 17.160点拨:由题图可知:长方形ABCD中去掉小路后,草坪正好可以拼成一个新的长方形,且它的长为米,宽为米.所以草坪的面积应该是长×宽=×=160. 18.10点拨:方程组2x-y=9-2k,② ①+②得,3x+y=15-k. 由于3x+y=5,所以15-k=5,解得k=10. 19.4 20.12;-144 3、21.解:原式=8-2-7=-2. 原式=-2-+3+-1=-2+3-1-+=0. 22.解:②×2得,6x+4y=26,③ ①-③得,y=5. 将y=5代入①得,6x+25=31,则x=1. 所以方程组的解为y=5. 解不等式①得,x<2; 解不等式②得,x≥-3. 所以不等式组的解集为-3≤x<2. 23.解:符合条件的三角形如图所示,点B的坐标为或. S△ABC=2×3×5=2. 24.解:40;162° “出色”的人数为40-2-8-18=12, 补全条形统计图如图. 40×480=216. 答:全年级男孩体质健康情况达到“好”的大约有216人. 25.解:55° ∠1+∠2=∠3.理由如下: ∵l1∥l2,∴∠1+∠PCD+∠PDC+∠2=180°. 在三角形PCD中,∠3+∠PCD+∠PDC=180°, ∴∠1+∠2=∠3. 由可知∠BAC=∠DBA+∠ACE=40°+45°=85°. 当P点在A的外侧时,∠3=∠2-∠1; 当P点在B的外侧时,∠3=∠1-∠2. 26.解:办法1、设饮用水有x件,则蔬菜有件, 依题意,得x+=320, 解这个方程,得x=200,x-80=120. 答:饮用水和蔬菜分别有200件、120件. 办法2、设饮用水有x件,蔬菜有y件,依题意,得x-y=80,解这个方程组,得y=120. 答:饮用水和蔬菜分别有200件、120件. 设租甲型货车n辆,则租乙型货汽车.依题意,得 10n+20(8-n)≥120, 解这个不等式组,得2≤n≤4. ∵n为正整数,∴n=2或3或4, ∴安排甲、乙两种型号的货车时有3种策略: ①安排甲型货车2辆,乙型货车6辆; ②安排甲型货车3辆,乙型货车5辆; ③安排甲型货车4辆,乙型货车4辆. 3种策略的运费分别为: 策略①:2×400+6×360=2 960; 策略②:3×400+5×360=3 000; 策略③:4×400+4×360=3 040. ∴策略①运费最少,最少运费是2 960元. 答:凯里某单位应选择安排甲型货车2辆,乙型货车6辆,可使运费最少,最少运费是2 960元. ![]()