周期型
1.电子跳蚤游戏盘是如图所示的
．假如跳蚤开始 时在
边的
处，
．跳蚤第一步从跳到
边的
（首次落点)处，且
；第二步从跳到
边的（首次落点)处，且
；第三步从跳到边的
（第三次落点)处，且
；……；跳蚤按上述规则一致跳下去，第n次落点为
（为正整数），则点
与
之间的距离为______．
答案：3
分析：依据规律：，
，
，
，
由此可得
，
，
，…
∴
．
故答案为3．
2.如图所示，长为，宽为
的长方形木板在桌面上做无滑动的翻滚（顺时针方向），木板上点地方变化为
，由
翻滚到时被桌面上一小木块挡住，此时长方形木板的边
与桌面成
角，则点翻滚到地方时所经过的路径总长度为__________
．
答案：
解
析：由
路径为
，由
路径为，因此由总路径为．故答案为：．
3.如图，正方形
边长为2cm，动点
从点出发，沿正方形的边按逆时针方向运动，当它的运动路程为2013cm时，线段的长为的形式，则
_____cm；当点第次（为正整数）到达点时，点的运动路程为____cm．
答案：5；8n-2，-2+8n
分析：
先求出正方形的周长，∵边长为
.
∴周长为.
再用2013除以8得到
.
即此时点已经从点运动了.
所以点的地方在
的中点，如图
则依据勾股定理
.
当点第1次到达点时，的运动路程为
；
当点第2次到达点时，的运动路程为；
当点第3次到达点时，的运动路程为
；
以此类推，
当点第
次到达点时，的运动路程为.
4.如图，菱形中，，,大家把菱形的
对称中心
称作菱形的中心．菱形在直线上向右作无滑动的
翻滚，每绕着一个顶点旋转叫一次操作，则经过
（
为正整数）
次如此的操作菱形中心所经过的路径总长为（ ）
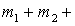
分析：
∵菱形中，，，
∴是等边三角形，，，[来源:Z。xx。k.Com]
首次旋转的弧长
，
∴1、二次旋转的弧长和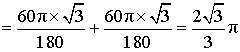
，
第三次旋转的弧长为：，
故经过（为正整数）次如此的操作菱形中心
所经过的路径总长为：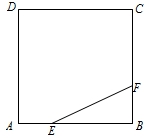
．
故答案为：，．
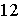5.察看下列等式：
解答下列问题： 的末位数字是（）
分析：∵
， ， ， ，
，
， …
∴末尾数，每
个一循环，
∵ ，
∴的末位数字等于：
的末尾数为
6.如图，动点 从 出发，沿所示的方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射
角，当点 第 次碰到矩形的边时，点 的坐标为（ ）
A．
B．
C．
D．
答案：D
分析：如下图，
动点 沿所示的方向运动，满足反弹时反射角等于入射角，
到①时，点 ；到②时，点 ；到③时，
点 ；到④时，点 ；到⑤时，点
；
到⑥时，点 ，此时回到出发点，继续.......，
出现每 次一循环碰到矩形的边.
由于 .
所以点 第 次碰到矩形的边时，点 的坐标为 .
故选 .
7.大家了解，一元二次方程没实数根，即没有一个实数的平方等于 ，若大家规定一个新数“”，使其满足 ，并且进一步规定: 所有实数可以与新数进行四则运算，且原有些运算律和运算法则仍然成立，于是有，，
，
那样， 的值为（ ）
A．
B．
C．
D．
答案：D
分析：因为
，
而，
.[来源:学科网]
8.如图，在直角坐标系中，已知点 、 ，对 连续作旋转变换，依次得到 、、
、
…，则的直角顶点的坐标为．
答案：8052；0
分析：∵ 、 ，
∴，
由图可知，每三个三角形为一个循环组依次循环，一个循环组前进的长度为： ，
∵，
∴的直角顶点是第个循环组的最后一个三角形的直角顶点，
∵ ，
∴的直角顶点的坐标为．
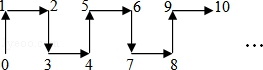
9.依据如图中箭头的指向规律，从到再到
，箭头的方向是以下图示中的
（ ）
选项：
A．B．C． D．
答案：D
分析：由图可知，每个数为一个循环组依次循环，
，
∴是第
个循环组的第个数，
∴从到再到，箭头的方向是．
故选 ．[来源:学_科_网]
10.有一个正六面体骰子，放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动 算一次，则滚动第 次后，骰子朝下一面的点数是______．
答案：3
分析：察看图象了解点数三和点数四相对，点数二和点数五相对且四次一循环，
∵ ，
∴滚动第次后与第二次相同，
∴朝下的点数为 ，
11.一列数 ，其中 ，，，…，
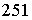，则
______．
答案： 1002
分析：，，
，，…，
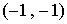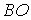由此可以看出三个数字一循环， ，
则
．
12.如图，弹性小球从点出发，沿所示方向运动，每当小球碰到矩形的边时反弹，反弹时反射角等于入射角，当小球第 次碰到矩形的边时的点为 ，第次碰到矩形的边时的点为 ，…，第 次碰到矩形的边时的点为，则点的坐标是___,点 的坐标是___．
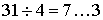
答案：8;3;5;0
分析：如图，
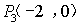
经过次反弹后动点回到出发点 ，
当点第次碰到矩形的边时，点的坐标为： ；
∵ ，
∴当点第次碰到矩形的边时为第个循环组的第次反弹，
点P的坐标为
．
13.在平面直角坐标系中，正方形的顶点分别为、
、
、
，
轴上有一点,作点关于点的对称点，作关于点
的对称点，作点关于点
的对称点，作关于点的对称点，作点关于点的对称点
，作关于点的对称点，按这样操作下去，则点的坐标为（ ）.
A．
B．
C．
D．
答案：D
分析：找出规律，，，，……，，，，.而除以余，所以点的坐标与坐标相同，为.
14.察看图中正方形四个顶点所标的数字规律，可知数应标在（）
A、第个正方形的左下角
B、第个正方形的右下角
C、第个正方形的左上角
D、第个正方形的右下角
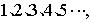
答案：C
分析：察看发现：正方形的左下角是的倍数，左上角是的倍数余，右下角是的倍数余，右上角是的倍数余.除以等于余，所以数应标在第个正方形的左上角.
15.如下表，从左到右在每一个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第个格子中的数为（）
分析：第一由已知和表求出、、，再察看找出规律求出第个格子中的数．
已知其中任意三个相邻格子中所填整数之和都相等，
则，，
，
解得
，，
按需要排列顺序为，，，，，，，…，[来源:学,科,网]
结合已知表得，
所以每一个小格子中都填入一个整数后排列是：，，，，，，…，
其规律是每个数一个循环.∵余，
∴第个格子中的数为.故选.
16.一个纸环链，纸环按红黄绿蓝紫的顺序重复排列，截去其中的一部分，剩下部分如图所示，则被截去部分纸环的个数可能是（）
分析：从图中知，该纸链是的倍数，中间截去的是剩下，从选项中数减为的倍数者即为所求.由于
被整除，故选.
17.若
，则的值为（ ）．（用含 的代数式表示）
分析：依据已知条件，找出题中的规律：
，
，
.
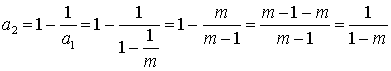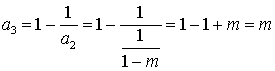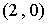可见，分别以，，循环.而 除以 余 ，从而的值与相同，为.
18.如下图，在平面直角坐标系中，对 进行循环往复的轴对称或中心对称变换，若原来点 坐标是，则经过第 次变换后所得的 点坐标是（ ）．
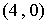
分析：由于变换是循环往复的，补全一个循环；
因此一个循环要经过 次变换.而 ……余 ，从而 经过第 次变换与经过第 次变换得到的地方相同，即在第四象限.由于原来点 坐标是（，），依据坐标关于 轴对称时，横坐标不变纵坐标改变符号的特征，得到经过第2011次变换后所得的A点坐标是（， ）.
19.将 、、
、
按如下方法排列．若规定（）表示第 排从左向右第 个数，则（ ）与（ ）表示的两数之积是（ ）．
分析： 从右边可见为.
下面求 是几：第一看是整个排列的第几个数，
从排列方法看第 排 个数，第 排 个数，……
第 排 个数，所以前 排一共的数目是
，
因此（ ）是第个数.
第二看第 个数是什么数，由于 、、、四个数循环，
而 商余 ，所以（）为.
则（ ）与（ ）表示的两数之积是.
20.如图物体从点 出发，根据（第步）（第步）
的顺序循环运动，
则第 步到达__________点处；
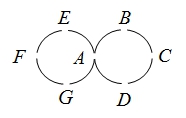
答案：D
分析：依据循环运动的规律，步一个循环.而 除以 余 ，故第步到达点处.
21.如图，将若干个正三角形、正方形和圆按肯定规律从左向右排列，那样第个图形是______．
答案：正方形．
分析：由图形看出去掉开头的两个三角形，剩下的由三个正方形，一个三角形，两个圆6个图形为一组，不断循环出现，，所以第 个图形是与循环的第二个图形相同是正方形．
22.将正方体骰子（相对面上的点数分别为和、和、和）放置于水平桌面上，如图①．在图②中，将骰子向右翻滚，然后在桌面上按逆时针方向旋转，则完成一次变换．若骰子的初始地方为图所示的状况，那样按上述规则连续完成次变换后，骰子朝上一面的点数是（）
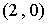
分析：不难看出经过一次变换后正面朝上的点数是，经过第二次变换后正面朝上的点数是，经过第三次变换后正面朝上的点数是，又回到了起始地方，则三个变换一循环，次变换即等于首次变换的结果故选B.
23.如图，圆圈内分别标有，，，…，这个数字，电子跳骚每跳一次，可以从一个圆圈跳到相邻的圆圈，目前，一只电子跳骚从标有数字“”的圆圈开始，按逆时针方向跳了次后，落在一个圆圈中，该圆圈所标的数字是______．
答案：
分析：依据题意可知是，，，，，…，即个数是一个循环．由于除余数为．故该圆圈所标的数字是
．故答案为：．
24.如图，在平面直角坐标系中，以原点O为圆心的同心圆半径由内向外依次为1，2，3，4，…，同心圆与直线和
分别交于，，，，…，则点的坐标是（ ）．
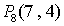
分析：本题考查知道直角三角形，一次函数等要点的应用，解此题的重点是确定出的地方．依据，得出在直线上，在第三象限，且在第8个圆上，求出，通过解直角三角形即可求出答案．
25.如图，菱形中，,大家把菱形的对称中心称作菱形的中心．菱形在直线上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过（为正整数）次如此的操作菱形中心所经过的路径总长为
分析：从图中可以看出，首次旋转是以点为圆心，那样菱形中心旋转的半径就是，解直角三角形可求出的长，圆心角是60度．第二次还是以点为圆心，那样菱形中心旋转的半径就是，圆心角是60度．第三次就是以点为旋转中心，为半径，旋转的圆心角为60度．旋转到此菱形就又回到了原图．故如此旋转18次，就是如此的6个弧长的总长，依此计算即可得，进而得出经过（为正整数）次如此的操作菱形中心所经过的路径总长．
26.如图，中， ，若为的中点,则的值为______；若边上有100个不一样的点，，…，，记，，…，，则…的值为______．
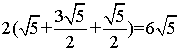
答案：4；400
分析：当在的中点时，可以得到直角三角形，借助勾股定理证明即可；第二个空可作
于．依据勾股定理，得，从而求得，即可求解．
27.如图所示，圆圈内分别标有1，2，…，12，这12个数字，电子跳蚤每跳一步，可以从一个圆圈逆时针跳到相邻的圆圈，若电子跳蚤所在圆圈的数字为，则电子跳蚤连续跳（）步作为一次跳跃，比如：电子跳蚤从标有数字1的圆圈需跳步到标有数字2的圆圈内，完成一次跳跃，第二次则要连续跳步到达标有数字6的圆圈，…依此规律，若电子跳蚤从①开始，那样第3次能跳到的圆圈内所标的数字为______；第2012次电子跳蚤能跳到的圆圈内所标的数字为______．
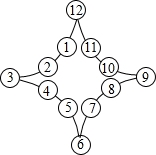
答案：10；6
分析：首次跳到数字2，第二次跳到数字6，第三次跳到数字10，第四次跳到数字2，…然后每三个一循环，用2012除以3，整除为10，余1为2，余2为6即可确定答案．
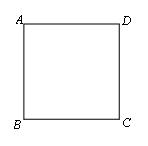
28.在数学校本活动课上，张老师设计了一个游戏，让电动娃娃在边长为1的正方形的四个顶点上依次跳动．规定：从顶点出发，每跳动一步的长均为1．首次顺时针方向跳1步到达顶点，第二次逆时针方向跳2步到达顶点，第三次顺时针方向跳3步到达顶点，第四次逆时针方向跳4步到达顶点，… ，以此类推，跳动第10次到达的顶点是______，跳动第2012次到达的顶点是______．
答案：；
分析：先依据每跳一次所到达的顶点，找出其中的规律是每八次一个循环，再用，即可求出跳动第10次到达的顶点，用，即可求出跳动第2012次到达的顶点．
29.察看下列图形的排列规律（其中☆、□、●分别表示五角星、正方形、圆）●□☆●●□☆●□☆●●□☆●…若第一个图形是圆，则第2009个图形是______．
答案：五角星
分析：依据题意剖析可得：圆、正方形、五角星前七个一组，依次循环；且2009除以7没余数；故第2009个图形是五角星．
30.如图，在平面直角坐标系中，一颗棋子从点处开始跳动，首次跳到点关于轴的对称点处，接着跳到点关于轴的对称点处，第三次再跳到点关于原点的对称点处，…，这样循环下去．当跳动第2009次时，棋子落点处的坐标是（______,______）．
答案：3；-2
分析：第一发现点P的坐标是，首次跳到点关于轴的对称点处是
，接着跳到点关于轴的对称点处是，第三次再跳到点关于原点的对称点处是…，发现3次一循环．又，则落在了处．
31.如图平面内有公共端点的五条射线从射线开始，在射线上写出数字1,2,3,4,5； 6,7,8,9,10；…．按此规律，则“12”在射线______上；“2011”在射线______上．
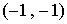
答案：；
分析：∵如图所示可知，每隔一个数正好是连续的有理数，∴11在上，∴“12”在射线上；∵每5个数一轮，2011÷5=402余数为1，每5轮顶点正好循环一周，402÷5=80余数为2，∴“2011”与第3轮第一个数的地方相同，即与9的地方相同，∴“2011”在射线 上．
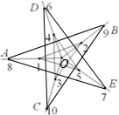
32.在平面直角坐标系中，矩形如图放置，动点从出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点第次碰到矩形的边时，点的坐标为（______,______）
答案：5；0
分析：依题可知，，，，，，，
，，，
个一循环，，故
故答案为：，．
33.如图，矩形的各边分别平行于轴或轴，物体甲和物体乙由点同时出发，沿矩形的边作环绕运动，物体甲按逆时针方向以个单位/秒匀速运动，物体乙按顺时针方向以个单位/秒匀速运动，则两个物体运动后的第次相遇地址的坐标是（_____,_____）
答案：-1；1
分析：依题可知，甲、乙两物体沿着矩形在做环形运动，矩形的周长为，秒，每过秒相遇一次，故首次在处相遇，第二次在处相遇，第三次在处相遇，第四次又在处相遇，故次一循环，，所以第次在处相遇．
故答案为：．
34.如图，正方形的边长为，点、分别在边、上，，小球从点出发沿直线向点运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当小球首次碰到边时，小球所经过的路程为__________；当小球首次碰到边时，小球所经过的路程为__________；当小球第（为正整数）次碰到点时，小球所经过的路程为__________．
分析：
；；
画图可知，次一个循环，一个循环周期，
所经过的路程为，
当小球第（为正整数）次碰到点时，
小球所经过的路程为．
故答案为：，，．
35.如图，在平面直角坐标系中，点，，
正六边形沿轴正方向无滑动滚动，当点首次落
在轴上时，点的横坐标为：_____；在运动过程中，点
的纵坐标的最大值是______；维持上述运动过程，经过
的正六边形的顶点是_____.
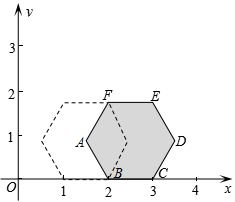
分析：由于，
所以经过的点势必会经过．
图分别是第二次和第三次滚动后的图形，
可以看出经过的点有、两个，
故经过为、两个点．
故答案为：，，或．
36.将正整数按以下方法排放：
则依据排放规律，从2002到2004的箭头依次为（ ）
分析：
数2002的地方与数2相同，数2003的地方与数3相同，数2004的地方与数4相同，
从2002到2004的箭头依次为
37.如图所示,两个全等菱形的边长为厘米,一只蚂蚁由点开始按的顺序沿菱形的边循环运动,行走厘米后停下,则这只蚂蚁停在（ ）点．
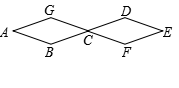
分析：
解：∵两个全等菱形的边长为厘米，[来源:学科网ZXXK]
∴蚂蚁由点开始按顺序走一圈所走的距离为厘米，
，
∴当蚂蚁走到第圈后再走厘米正好到达点。
故答案为：C。
