2019学年上海初一首次月考数学试题(2)

初一（下）首次月考数学试题

1、选择题（本大题共12小题，每题3分，共36分）

1．（3分）如图，数轴上A，B，C，D四点中，与对应的点距离近期的是（）

A．点A B．点B C．点C D．点D

2．（3分）国内是一个干旱缺水紧急的国家．国内的淡水资源总量为28000亿立方米，占全球水资源的6%，仅次于巴西、俄罗斯和加拿大．用科学记数法表示28000亿是（）

A．2.8×104 B．28×103 C．28×1011 D．2.8×1012

3．（3分）下列方程组中不是二元一次方程组的是（）

A． B．

C． D．

4．（3分）单项式的系数与次数分别为（）

A．﹣3和5 B．和5 C．和6 D．和5

5．（3分）在下列实数中：﹣0.6，，，，，0.010010001……，3.14，无理数有（）

A．2个 B．3个 C．4个 D．5个

6．（3分）以方程组的解为坐标的点（x，y）在平面直角坐标系中的地方是（）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

7．（3分）某中学组织初中一年级部分学生参加社会实践活动，需要租用若干辆客车．若每辆客车乘40人，则还有10人不可以上车；若每辆客车乘43人，则只有1人不可以上车．设租了x辆客车，则可列方程为（）

A．40x+10＝43x+1 B．40x﹣10＝43x﹣1

C．40x+10＝43（x﹣1） D．40x+10＝43x﹣1

8．（3分）已知点P（a，b）在第三象限，且|a|＝3，|b|＝4，那样点P的坐标为（）

A．（﹣4，﹣3） B．（﹣3，﹣4） C．（﹣3，4） D．（3，﹣4）

9．（3分）下列说法：

①两点之间的所有连线中，线段最短；

②相等的角是对顶角；

③过直线外一点有且仅有一条直线与已知直线平行；

④两点之间的距离是两点间的线段．

其中正确的个数是（）

A．1个 B．2个 C．3个 D．4个

10．（3分）上午9点30分时，钟面上时针与分针所成的角的度数是（）

A．115° B．105° C．100° D．90°

11．（3分）如图，AE平分∠BAC，CE平分∠ACD，有下列条件：①∠1＝∠2；②∠1+∠2＝90°；③∠3+∠4＝90°；④∠2+∠3＝90°；其中能断定AB∥CD的有（）

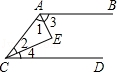
A．1个 B．2个 C．3个 D．4个

12．（3分）如图，平面直角坐标系内放置一个直角梯形AOCD，已知AD＝6，AO＝18，OC＝12，若点P在梯形内，且S△PAD＝S△POC，S△PAO＝S△PCD，那样点P的坐标是（）

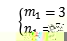
A．（5，4） B．（5，6） C．（5，8） D．（8，4）

2、填空题（本大题共6小，每题3分，共18分）

13．（3分）的平方根是__________．

14．（3分）关于xy的方程x2m﹣n﹣2+7ym+1＝4是二元一次方程，则：m+n＝__________．

15．（3分）已知线段AB∥y轴，AB＝3，A点的坐标为（﹣1，2），则点B的坐标为__________．

16．（3分）已知4﹣2a2+a＝0，则4a2﹣2a﹣3的值为__________．

17．（3分）已知：如图，∠AOB＝168°，OD是∠AOC的平分线，OE是∠BOC的平分线，那样∠DOE等于__________．

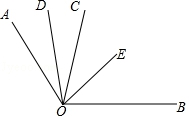
18．（3分）如图，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为Pn，点P2019的坐标是__________．

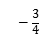
3、解符烟（本大题共8小题，19、20每题6分，21、22每题8分，23、24每题9分，25、26每题10分，共66分）

19．（6分）求下列各式中的x．

（1）（1﹣2x）2＝169；

（2）（3x﹣2）3＝64．

20．（6分）计算或解方程组

（1）|1|；

（2）．

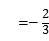21．（8分）已如A是n﹣m+3的算术平方根，B是m+2n的立方根，求B+A的平方根．

22．（8分）已知：A（0，1），B（2，0），C（6，4）．

（1）求△ABC的面积；

（2）设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．

23．（9分）列方程或方程组解应用题：为大力弘扬和传承雷峰精神，推进学雷锋志愿服务活动深入拓展，3月1日我校校团委组织了第六届以“集结爱心 传递真情”为主题的爱心义卖活动，在本次爱心义卖活动中，初中一年级（1）班小王同学供应甲乙两种不同型号的笔记本，已知1本甲种笔记本和1本乙种笔记本共需要8元，2本甲种笔记本和3本乙种笔记本共需要21元．

（1）求甲乙笔记本的单价分别为多少元？

（2）小王同学在本次爱心义卖活动中，供应甲乙笔记本总收入49元，若假设甲笔记本数目为m本，乙笔记本数目为n本，求m、n的值．

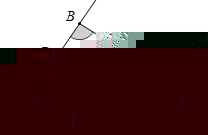
24．（9分）已知：如图，点D是直线AB上一动点，连接CD．

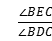
（1）如图1，当点D在线段AB上时，若∠ABC＝105°，∠BCD＝30°，求∠ADC度数；

（2）当点D在直线AB上时，请写出∠ADC、∠ABC、∠BCD的数目关系，并证明．

25．（10分）当m，n都是实数，且满足2m＝8+n，就称点P（m﹣1，）为“爱心点”．

（1）判断点A（5，3），B（4，8）什么点为“爱心点”，并说明理由；

（2）若点A（a，﹣4）、B（4，b）是“爱心点”，请判断A、B两点的中点C在第几象限？并说明理由；

（3）已知p，q为有理数，且关于x，y的方程组解为坐标的点B（x，y）是“爱心点”，求p，q的值．

26．（10分）在平面直角坐标系中，A（a，0），B（b，4），C（c，0）其中a，b，c满足关系|a﹣b+4|+（c﹣5）2＝0．

（1）如图1，求△ABC的面积；

（2）如图2，在x负半轴上有一点D，满足DB⊥BC，∠BCD的角平分线与∠BDC的角平分线相交于点P，点E是CP延长线上一点，且满足∠EBD＝45°，求的值；

（3）如图3，若将线段AB向上平移1个单位长度，点G为x轴上一点，点F（5，n）为第一象限内一动点，连BF、CF、CA，若△ABG的面积等于由AB、BF、CF、AC四条线段围成图形的面积，求点G点坐标（用含n的式子表示）．

初一（下）首次月考数学试题

参考答案

1、选择题（本大题共12小题，每题3分，共36分）

1．B； 2．D； 3．C； 4．D； 5．B； 6．D； 7．A； 8．B； 9．B； 10．B； 11．C； 12．B；

2、填空题（本大题共6小，每题3分，共18分）

13．__________； 14．__________； 15．__________； 16．__________； 17．__________； 18．__________；

3、解符烟（本大题共8小题，19、20每题6分，21、22每题8分，23、24每题9分，25、26每题10分，共66分）

19．解：（1）开平方，得 1﹣2x＝13或1﹣2x＝﹣13，

∴x＝﹣6或x＝7；

（2）开立方，得 3x﹣2＝4，

∴x＝2．

20．解：（1）原式＝9+3+21

＝13；

（2）将方程组整理成一般式得：，

②﹣①得：x＝﹣6，

把x＝﹣6代入①得：﹣12+y＝3，

∴y＝15，

∴．

21．解：由题意可得，

∴，

∴A，

B，

∴B+A的平方根为．

22．解：（1）如图S△ABC＝4×61×26×34×4＝6．

（2）①当点P在x轴上时，设P（m，0），则有•|2﹣m|•1＝6，解得m＝﹣10或14，

∴P（﹣10，0）或（14，0）．

①当点P在y轴上时，设P（0，n），则有•|1﹣n|•2＝6，解得n＝7或﹣5，

∴P（0，7）或（0，﹣5）．

23．解：（1）设甲种笔记本的单价为x元/本，乙种笔记本的单价为y元/本，

依题意，得：，

解得：．

答：甲种笔记本的单价为3元/本，乙种笔记本的单价为5元/本．

（2）∵甲笔记本数目为m本，乙笔记本数目为n本，

∴3m+5n＝49，

∴n．

∵m，n均为正整数，

∴，，．

答：m，n的值为3，8或8，5或13，2．

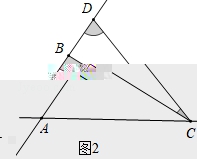
24．解：（1）如图1中，

∵∠ADC＝∠ABC+∠BCD，∠ABC＝105°，∠BCD＝30°，

∴∠ADC＝135°．

（2）如图1中，当点D在线段AB上时，∠ADC＝∠ABC+∠BCD．

如图2中，当点D在线段AB的延长线上时，∠ABC＝∠ADC+∠BCD．

如图3中，当点D在线段BA的延长线上时，∠ADC+∠ABC+∠BCD＝180°．

25．解：（1）A点为“爱心点”，理由如下：

当A（5，3）时，m﹣1＝5，3，

解得m＝6，n＝4，则2m＝12，8+n＝12，

所以2m＝8+n，

所以A（5，3）是“爱心点”；

当B（4，8）时，m﹣1＝4，8，

解得m＝5，n＝14，显然2m≠8+n，

所以B点不是“爱心点”；

（2）A、B两点的中点C在第四象限，理由如下：

∵点A（a，﹣4）是“爱心点”，

∴m﹣1＝a，4，

解得m＝a+1，n＝﹣10．

代入2m＝8+n，2（a+1）＝8﹣10，解得a＝﹣2，

所以A点坐标为（﹣2，﹣4）；

∵点B（4，b）是“爱心点”，

同理可得m＝5，n＝2b﹣2，代入2m＝8+n，解得b＝2．

所以点B坐标为（4，2）．

∴A、B两点的中点C坐标为（，），即（1，﹣1），在第四象限．

（3）解关于x，y的方程组得．

∵点B（x，y）是“爱心点”，

∴m﹣1p﹣q，2q，

解得mp﹣q+1，n＝4q﹣2．

代入2m＝8+n，得2p﹣2q+2＝8+4q﹣2，

整理得2p﹣6q＝4．

∵p，q为有理数，若使2p﹣6q结果为有理数4，

则P＝0，所以﹣6q＝4，解得q．

所以P＝0，q．

26．解：（1）∵|a﹣b+4|+（c﹣5）2＝0．

∴，解得：，

∴A（﹣2，0），B（2，4），C（5，0），

∴△ABC的面积14；

（2）如图2，∵DB⊥BC，

∴∠DBC＝90°，

∴∠BDC+∠BCD＝90°，

∵DP平分∠BDC，PC平分∠BCD，

∴∠PDC∠BDC，∠PCD∠BCD，

∴∠PDC+∠PCD（∠BDC+∠BCD）＝45°，

∴∠EPD＝∠PDC+∠PCD＝45°，

∵∠EBD＝∠EPD＝45°，∠EMB＝∠DMP，

∴∠BEC＝∠BDP，

∴；

（3）如图3，平移后的点A（﹣2，1），B（2，5），

将四边形ABFC拓展成长方形HDCM，

则S四边形ABFC＝S长方形HDCM﹣S△ABH﹣S△ADC﹣S△BFM，

＝7×5（5+2）×1，

＝16n，

设G（x，0），分两种状况：

①当点G在x轴的正半轴上时，如图3，延长BA交x轴于点R，

同理得：S△ABG＝5（x+2）2x+6，

∵S△ABG＝S四边形ABFC，

∴2x+6＝16n，

x＝5n，

∴G（5n，0）

②当点G在x轴的负半轴上时，如图4，同理作长方形MGNB，过A作AQ⊥NB于Q，

∴S△ABG＝5（2﹣x）2x﹣6，

∵S△ABG＝S四边形ABFC，

∴﹣2x﹣6＝16n，

x＝﹣11n，

∴G（﹣11n，0）

综上，点G的坐标为：（5n，0）或（﹣11n，0）．