2020-2021学年度静安区市北初级中学初一（上）数学第二次月考考试试题
（完卷时间90分钟，满分100分） 2019.12
1、选择题：（本大题共6题，每题2分，满分12分）
1.在下面四个式子中，为代数式的是（ ）
A.0 B.
C.s=vt D.a+b=b+a
2.下列算式中，正确的是（ ）
A.x3+x3=x6 B.-1=x+y
C.
D.6•3=-a6b3
3.下列算式中，正确的是（ ）
A.=a2-2 B.2=a2-9b2
C.=mp-mq+np-nq D.=x2-x-6
4.如kg把分式
中的a、b同时扩大为原来的2倍，那样得到的分式的值（ ）
A.扩大为原来的4倍 B.扩大为原来的2倍
C.缩小到原来的
D.不变
5.下列说法正确的是（ ）
A.平移和旋转的一同点是改变了图形的地方，而图形的形状、大小没变化。
B.平移不改变图形的形状、大小，而旋转则改变图形的形状、大小。
C.图形可以向某方向平移一段距离，也可以向某方向旋转一段距离。
D.在平移和旋转图形中，对应角相等，对应线段相等且平行。
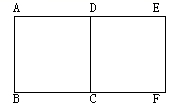
6.如图1，假如正方形ABCD旋转后能与正方形CDEF重合，那样图形所在的平面内可作族转中心的点共（ ）
A.1个 B.2个 C.3个 D.4个
2、填空题:
7.假如单项式3xn-1y4与x3ym是相同种类项，那样n-m的值是__________。
8.计算:-=__________。
9.计算：-y2·3=__________。
10.计算：=__________。
11.计算：÷=__________。
12.分解因式：a2+5a-6=__________。
13.若1厘米=10000微米，则2微米=__________厘米。
14.若分式
有意义，则x的取值范围是__________。
15.计算：
__________。
16.分式方程
的解为__________。
17.计算：÷=
18.如图2，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为__________cm。
19.如图3，将△ABC绕着点A顺时针旋转后能与△ADE，且∠BAE=58º,则旋转角的大小是__________。
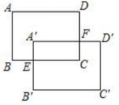
20.如图4，在长方形ABCD中，AB=7cm,BC=10cm,现将长方形ABCD向右平移3cm，再向下平移4cm后到长方形A´B´C´D´的地方，A´B´交BC于点E，A´D´交DC于点F,那样长方形A´ECF的周长为__________cm。
3、简答卷：（本大题共6题，每题6分，满分36分）
21.计算：•
x2y+3+3 22.计算：
（结果不含负整数指数幂）
23.分解因式：2-7-8 24.分解因式：a2-4+4b2-4ab
25.解方程：
先化简，再求值：
，其中x=-2.
4、解答卷
27.在图5中的网格上按需要画出图形，
并回答问题:
假如将三角形ABC平移，使得点
A平移到图中点D地方，点B、点C
的对应点分别为点E、点F，
请画出三角形DEF；
画出三角形ABC关于点D成中心
对称的三角形A1B1C1；
三角形DEF与三角形A1B1C1__________
关于某个点成中心对
称?若是，请在图中画出这个对称中心，
并记作点O。
28.某人骑自行车比步行每小时多走8千米，假如他步行12千米所用的时间与骑自行车36千米所用的时间相等.求他骑自行车的速度。
29.如图6，已知长方形ABCD与正方形BEFM，且A、B、E在一直线上，已知AB＝a，BC＝b，BE＝c，且a＞b＞c＞0.设△ADE的面积为S1。
用含a、b、c的代数式表示S1；
正方形BEFM绕B顺时针旋转180度得到正方形BE´F´M´，连接DM´，用含a、b、c的代数式表示△DCM´的面积为S2;
请比较S1与S2的大小关系，并说明理由.
30.如图7，长方形OABC的边OA在数轴上，O为原点，长方形OABC的面积为12，OC边长为3.
数轴上点A表示的数为__________.
将长方形OABC沿数轴水平移动，移动后的长方形记为O´A´B´C´，移动后的长方形O´A´B´C´与原长方形OABC重叠部分的面积记为S。
①当S恰好等于原长方形OABC面积的一半时，数轴上点A´表示的数是__________.
②设点A的移动距离AA＇＝x
当S＝4时，求x的值；
D为线段AA´的中点，点E在找段OO＇上，且OO＇＝3OE，当点D，E所表示的数互为相反数时，求x的值。
