2018年上海曹杨二中高中三年级周测试题
2018年1月2日
1、填空题（54分）
1、已知集合
，则
_____________；
2、已知等差数列
的前
项和为
，若
，
，则
_____________；
3、若正整数满足，则行列式
的值为_____________；
4、已知
，为单位向量，且
，则向量，的夹角为____________；
5、双曲线
的两条渐近线的夹角为___________________；
6、若复数
满足（
为虚数单位），且在复平面内对应的点坐落于第一象限，则实数
的取值范围是_____________；
7、已知正三棱锥的底面边长为4，高为2，则其表面积为_______________；
8、若展开式中的二项式系数之和为128，则展开式中系数最小的项为____________；
9、在中，
，则角
的最大值为_______________；
10、5名学生到地铁站参加志愿者活动，该地铁站4个出口，需要每一个出口至少有一名志愿者服务，则不同安排办法有___________种。
11、设正实数
，，
满足
，则的最大值为________；
12、设函数
、
的概念域均为，若对任意
，且，具备
，则称函数为上的单调非减函数，给出以下命题：
①若为周期函数，则不可能是单调非减函数；
②若既是周期函数又是单调非减函数，则肯定是常值函数；
③若单调非减函数，且关于无穷多个点中心对称，则得图像是一条直线；
④若单调非减函数，却关于无穷多条平行于
轴的直线对称，则是常值函数.
以上命题中，所有真命题的序号是__________________.
2、选择题（20分）
13、“点
在曲线
上”是“点的坐标满足方程
”的（ ）
A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分也非必要条件
14、在空间中，设、是不一样的直线，
、
是不一样的平面，且
，，则下列命题正确的是（ ）
A、若
，则 B、若、异面，则、平行
C、若、相交，则、相交 D、若，则
15、在中，
，，其中，是常数，满足
，那样
的值（ ）
A、可能没有 B、有且仅有一个 C至少一个 D、至少两个
16、已知函数，给出下列四个判断：
①的值域是
②的图像是轴对称图形
③的图像是中心对称图形 ④方程
有解
其中正确的判断有（ ）
A、1个 B、2个 C、3个 D、4个
3、解答卷（76分）
17、如图，在四棱锥中，
平面
，底面是菱形，且
，
.
（1）求证：平面；
（2）若，求
与平面
所成角的大小（用反三角函数值表示）。
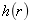
18、如图摄影喜好者在某公园
出发现正前方处由一立柱，，测得立柱顶端
的仰角和立柱底部的俯角均为，设的双眼距离底面的距离为米。
（1）求甚至到立柱的水平距离和立柱的高度；
（2）立柱的顶端有一长2米的彩杆绕其中点在于立柱所在的平面内旋转，摄影者有一视角范围为的镜头，在彩杆转动的任意时刻，摄影者是不是都可以将彩杆全部摄入画面？说明理由。
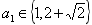
19、在直角坐标系
中，两动圆和
，记它们公共点的轨迹为曲线
.
（1）求曲线的方程；
（2）若上的相异两点，满足
，求证：到的距离为定值.
20、已知函数，无穷数列满足
，
.
（1）若
，求数列的通项公式；
（2）若，求的取值范围；
（3）若成等比数列，求的取值范围.
21、已知函数.
（1）若
，求的值；
（2）设
，当时，的值域为，试求与的值；
（3）当
时，记，若对于区间
上的任意三个实数，都存在以、
、为边长的三角形，求实数的取值范围.
参考答案：
1、填空题：
1、；2、
；3、；4、；5、；6、；7、
；
8、
；9、；10、；11、
；12、②④；
2、选择题：
13、B；14、C；15、C；16、B；
3、解答卷：
17、（1）略；（2）；
18、水平距离：3米，高：米；（2）可以全部摄入画面；
19、（1）；（2）定值为：，证明略；
20、（1）；（2）
；（3）；
21、（1）20；（2）
，；（3）
；
