7.翻折问题
1.在
中，
，
，
为
延长线上一点，
为
内部一点，且
．
（1）若
，如图1，直接写出
间的数目关系：___________；
（2）若
，如图2，求证：
；
（3）在（2）的条件下，如图3，将线段
沿
翻折，翻折后的点
落在点
处，且
，连接
，交的延长线于
，若
，求
的长．
分析：（1）
提示：作
于
，
交
延长线于
∵，
∴
∵
∴，
∴
∴
∴
∴
，
∴
∴
（2）作于，交延长线于[来源:学,科,网]
∵，
∴
∵
∴
，
∴
∴
，
∴，
∴
∴，
∴
∴
（3）作于，于
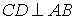
则，
由题意，
∴，
∴
∴
∵，
∴
∴
，
∴
∴
由（2）知，，
∴
∵，
∴，
∴
，
∴
∴
，
∴
∴，
∴
∴
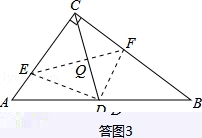
2.如图，在中，，翻折，使点
落在斜边
上某一点处，折痕为（点
分别在边
上）
（1）若与相似．
①当时，求的长；
②当时，求的长；
（2）当点是的中点时，与相似吗？请说明理由．
分析：（1）若与相似．
①当时，为等腰直角三角形，如答图1所示．
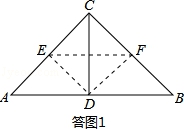
此时为边中点，．
②当时，有两种状况：
（I）若
，如答图2所示．
∵，
∴．
由折叠性质可知，，
∴，即此时为边上的高．
在中，，
∴，
∴
．
；
（II）若
，如答图3所示．
∵，
∴．
由折叠性质可知，，
又∵，
∴，
∴．
同理可得：
，
∴此时
．
综上所述，当时，的长为或．
（2）当点是的中点时，与相似．理由如下：
如答图3所示，连接，与交于点
．
∵是的中线，
∴，
∴．
由折叠性质可知，，
∴，
∵，
∴，
又∵，
∴．
3.在矩形
中，，点分别在边上，且
．点为边上的一个动点，连接，把沿直线翻折得到．
（1）如图1，当时，
①填空：
___________度；
②若
，求的度数，并求此时的最小值；
