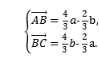第3课时平面向量的数乘运算及其几何意义
基础达标
1.若m∈R,则下列说法正确的是.
A.若ma=0,则m=0
B.若m≠0,a≠0,则ma与a方向相同
C.若m≠0,a≠0,则|ma|=m|a|
D.若m≠0,a≠0,则ma与a共线
【分析】由ma=0得m=0或a=0,故A错;当m≠0时,ma与a方向相同或相反,故B错;当m≠0,a≠0时,|ma|=|m||a|,故C错.
【答案】D
2.设e1,e2是两个不共线的向量,若向量m=-e1+ke2与向量n=-2e1+e2共线,则k等于.
A.0B.
C.1D.2
【分析】由m与n共线,得m=λn,所以-e1+ke2=-2λe1+λe2,即e1+e2=0,故
解得k=.
【答案】B
3.已知向量a,b不共线,且
=a+2b,
=-5a+6b,
=7a-2b,则共线的三点是.
A.A,B,D B.A,B,C
C.B,C,D D.A,C,D
【分析】∵
=
+
=+=2a+4b,∴=2
,∴A,B,D三点共线.故选A.
【答案】A
4.在△ABC所在平面上有一点P,满足+
+
=,则△PBC与△ABC的面积之比是.
A.
B. C.
D.
【分析】由
+
+
=,得++
+=0,即=2,所以点P是AC边上挨近点A的三等分点,故
=.
【答案】C
5.已知
=3,=3,则
与
__________.
【分析】由于
=3,=3,
所以
=+
=3+3=3=3
,
所以与共线.
【答案】共线
6.已知点C在线段AB上,=,=λ,则λ=__________.
【分析】=
=
=
+
=-
,即=-,故=-
.
【答案】-
7.已知e,f为两个不共线的向量,若四边形ABCD满足=e+2f,=-4e-f,=-5e-3f.
用e,f表示;
证明四边形ABCD为梯形.
【分析】由题意,有=++=++=e+f=-8e-2f.
由知=-8e-2f=2=2,即=2.
依据数乘向量的概念,与同方向,且的长度为的长度的2倍,所以在四边形ABCD中,AD∥BC,且AD≠BC,所以四边形ABCD为梯形.
拓展提高
8.设a是非零向量,λ是非零实数,则下列结论正确的是.
A.a与-λa的方向相反
B.|-λa|≥|a|
C.a与λ2a的方向相同
D.|-λa|=|λ|a
【分析】若λ>0,则a与-λa的方向相反;若λ<0,则a与-λa的方向相同,A错误.若|λ|<1,则|-λa|<|a|,B错误.|-λa|是一个大于或等于零的实数,而|λ|a是向量,它们之间不可以比较大小,D错误.
【答案】C
9.若O是平面上肯定点,A,B,C是平面上不共线的三个点,动点P满足
=+λ,λ∈[0,+∞),则点P的轨迹肯定经过△ABC的.
A.外心 B.内心 C.重心 D.垂心
【分析】由点P满足的条件,可得
-
=λ,即=λ,所以与
+共线,其中与分别是与的单位向量.又由平行四边形法则,可得
+与∠BAC的平分线共线.如图所示,AD为其角平分线,所以与共线.由于λ∈[0,+∞),所以点P的轨迹肯定经过△ABC的内心,故选B.
【答案】B
10.在平行四边形ABCD中,E,F分别在边DC,AB上,且DE=DC,AF=
AB,则与的关系是__________.
【分析】如图,设=a,=b,由于DE=
DC,AF=
AB,所以=+=a+b,
=
+
=-=-.
【答案】=-
11.已知▱ABCD的边BC,CD的中点分别是M,N,设
=a,
=b,试用a,b表示向量,.
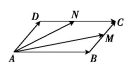
【分析】∵在▱ABCD中,M,N分别是边BC,CD的中点,
∴
=
,
=.
∴=+=+,=+,
∴
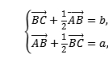解得
