人教版数学初三上册 第21章 一元二次方程 单元综合练习题
1.一元二次方程x2-3x-2=0的两根为x1,x2,则下列结论正确的是
A.x1=-1,x2=2 B. x1=1,x2=-2
C.x1+x2=3 D. x1x2=2
2.已知x1,x2是一元二次方程x2-4x+1=0的两个根,则x1·x2等于
A.-4 B.-1 C.1 D.4
3.已知关于x的一元二次方程x2-2x-k=0有两个不相等的实数根,则实数k的取值范围是
A.k≥1 B.k>1 C.k≥-1 D.k>-1
4.一元二次方程2-22=7的根的状况是
A.无实数根 B.有一正根一负根 C.有两个正根 D.有两个负根
5.下列一元二次方程没实数根的是
A.x2+2x+1=0 B.x2+x+2=0
C.x2-1=0 D.x2-2x-1=0
6.依据下列表格中的对应值,判断方程ax2+bx+c=0的根的个数是
x | 6.17 | 6.18 | 6.19 | 6.20 |
y=ax2+bx+c | 0.02 | 0.01 | 0.02 | 0.04 |
A.0 B.1 C.2 D.1或2
7.关于x的一元二次方程x2-x+sinα=0有两个相等的实数根,则锐角α等于
A.15° B.30° C.45° D.60°
8. 方程x2-3=0的根是________________________________________________________________.
9.已知关于x的方程x2+3x+a=0有一个根为-2,则另一个根为______________.
10.关于x的一元二次方程x2+bx+2=0有两个不相等的实数根,写出一个满足条件的实数b的值:b=______________.
11.已知关于x的一元二次方程x2+2x-=0有实数根,则m的取值范围是______________
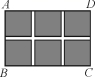
12.如图,某小区规划在一个长30 m,宽20 m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78 m2,那样通道的宽应设计成多少?设通道的宽为x m,由题意列得方程______________.
13.将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成|cd|,概念|cd|=ad-bc,上述记号就叫做2阶行列式.若|1-xx+1|=8,则x=______________.
14.解方程:22=x2-9
解:x1=3,x2=9
15. 已知关于x的一元二次方程·=|m|.
求证:对于任意实数m,方程总有两个不相等的实数根;
若方程的一个根是1,求m的值及方程的另一个根.
解:Δ=1+4|m|>0,所以总有两个不等实数根
m=2或m=-2;另一个根为x=4
16.一幅长20 cm、宽12 cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为x cm,图案中三条彩条所占面积为y cm2.
求y与x之间的函数关系式;
若图案中三条彩条所占面积是图案面积的5,求横、竖彩条的宽度.
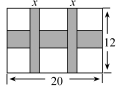
解:依据题意可知,横彩条的宽度为2x cm,
∴y=20×2x+2×12·x-2×2x·x=-3x2+54x,
即y与x之间的函数关系式为y=-3x2+54x;
依据题意,得:-3x2+54x=5×20×12,
整理,得:x2-18x+32=0,解得:x1=2,x2=16,
∴2x=3,
则横彩条的宽度为3 cm,竖彩条的宽度为2 cm
17.某市首条绿道免费公共自行车出租系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.以后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
请问每一个站点的造价和公共自行车的单价分别是多少万元?
请你求出2016年到2018年市政府配置公共自行车数目的年平均增长率.
解:设每一个站点造价x万元,自行车单价为y万元.依据题意可得
120x+2205y=340.5,解得y=0.1,
则每一个站点造价为1万元,自行车单价为0.1万元.
设2016年到2018年市政府配置公共自行车数目的年平均增长率为a.
依据题意可得7202=2205,
整理得2=16,
解得a1=4=75%,a2=-4,
则2016年到2018年市政府配置公共自行车数目的年平均增长率为75%
18.已知关于x的一元二次方程x2+2bx+=0,其中a,b,c分别为△ABC三边的长.
假如x=-1是方程的根,试判断△ABC的形状,并说明理由;
假如方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
假如△ABC是等边三角形,试求这个一元二次方程的根.
解:△ABC是等腰三角形;理由:∵x=-1是方程的根,∴×2-2b+=0,∴a+c-2b+a-c=0,∴a-b=0,∴a=b,∴△ABC是等腰三角形
∵方程有两个相等的实数根,∴2-4=0,∴4b2-4a2+4c2=0,∴a2=b2+c2,∴△ABC是直角三角形
当△ABC是等边三角形,∴x2+2bx+=0可整理为2ax2+2ax=0,∴x2+x=0,解得x1=0,x2=-1
19. 在某市组织的大型商业演出活动中,对团体购买门票实行打折,决定在原定票价基础上每张降价80元,如此按原定票价需花费6 000元购买的门票张数,目前只花费了4 800元.
求每张门票原定的票价;
依据实质状况,活动组织单位决定对于个人购票也采取打折手段,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
解:设每张门票原定的票价为x元,由题意得x=x-80,
解得x=400.经检验,x=400是原方程的解,
则每张门票原定的票价400元
设平均每次降价的百分率为y.由题意得4002=324,
解得y1=0.1,y2=1.9,则平均每次降价10%







