徐汇区南洋模范中学初二（上）数学第二次月考试题
1、选择题
1.
的有理化因式是…………………………………………………………（ ）
2.下列方程中,没实数根的方程是……………………………………………（ ）
3.假如正比率函数图像与反比率函数图像的一个交点的坐标为,那样另一个交点的坐标为……………………………………………………………………（ ）
4.下列定理中,没逆定理的是…………………………………………………（ ）
两直线平行,同旁内角互补 两个全等三角形的对应角相等;
直角三角形的两个锐角互余 两内角相等的三角形是等腰三角形
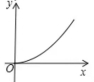
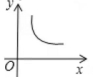
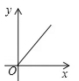
5.甲乙两地相距100千米,某人开车从甲地到乙地,则他的平均速度y与时间x之间的关系用图像大致可表示为…………………………………（ ）
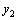
6.如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△
若两个三角形重叠部分的面积为1cm2,则它移动的距离
等于…………………………………………………………………………………（ ）
0.5cm 1cm 1.5cm 2cm
填空题
7.计算:
__________.
8.假如函数,那样
__________.
9.函数
的概念域是__________.
10.方程
的解是__________.
11.在实数范围内分解因式
__________.
12.已知点
在第四象限,则正比率函数
图像经过第__________象限.
13.若反比率函数
)
随
的增大而减小,则m的取值范围是__________.
14.过A、B两点的圆的圆心的轨迹是__________.
15.已知等腰三角形的周长为20,腰长是方程
的一个根,则这个等腰三角形的腰长为__________.
16.在Rt△ABC中,∠C=90°,∠A的平分线交C于点D且AC=5,AB=10,△ABC面积为15,那样点D到AB的距离等于__________.
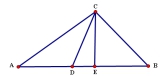17.如图,在Rt△ABC中,∠ACB=90°,∠A=35°,D为AB边上的中点,CE⊥AB,那样∠DCE=__________.
18.△ABC的三边AB、BC、CA的长分别是2、30、40,其三条角平分线相交于O点，将三角形ABC分为三个三角形，则
__________.
3、简答卷
19.计算：
20.解方程：
在实数范围内分解因式：
先化简，后计算：，其中
已知
,
与成正比率,与成反比率,且当
时,
,当
时,
,求与之间的函数关系.
如图,在△ABC中,DF垂直平分AB于点D,交C于点E,交BC的延长线于点F,且AB=EF,∠A:∠F=4:3,∠A的度数
3、解答卷
25.某养殖户每年的养殖本钱包含固定本钱和可变本钱,其中定本钱每每年平均为4万元,可变本钱逐年增加,已知该养殖户第一年的可变本钱为2.6万元,设可变本钱平均每年增长的百分率为
用含的代数式表示第3年的可变本钱为__________.
假如该养殖户第3年的养殖本钱为7.146万元,求可变本钱平均每年增长的百分率
26.据医学研究,用某种抗生素治疗心肌炎,人体内每毫升血液中的含药量不少于4微克时,治疗有效.假如一病人按规定剂量服用这种抗生素,服用后每毫升血液中的含药量与服用后的时间之间的函数关系如图所示:
假如上午8时服用该药物,到__________时该药物的浓度达到最大值__________微克/毫升;
依据图象求出从服用药物起到药物浓度最高时y与t之间的函数分析式;
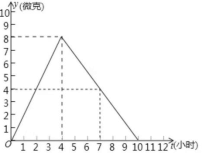
假如上午8时服用该药物,到__________时该药物开始有效，有效时间一共是__________小时;
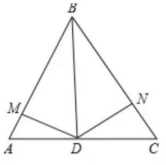
27、如图,在△ABC中,BD平分∠ABC,M、N分别是BA、BC上的点,且∠MDN+∠MBN=180°.
求证:DM=DN
5、综合题
28、如图,在平面直角坐标系中,直线
与双曲线
交于点
求
和
值
过轴的点
作平行于轴的直线,分别于直线与双曲线
交于点P、Q,求△OPQ面积
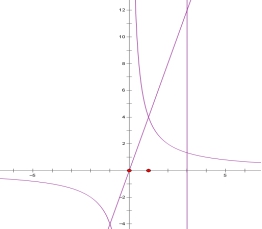依据图像,写出正比率函数值大于反比率函数值的的取值范围
