浦东区进才北校初二（上）数学第二次月考考试试题
选择题
1.下列各式:
，
,
,
, 
,其中是二次根式的个数有（ ）
A.2个 B.3个 C.4个. D.5个
2.以下列各组数为边长的三角形中,可以构成直角三角形的是（ ）
A.
,
,
; B.2,
,
; C.1,
, 
; D.,,
.
3.《九章算术》中的“折竹抵地”问题:今有竹高-丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子原高中一年级丈 ,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺，则可列方程（ ）
-6=
; B.
-
=;
=; D. +=
4.已知关于x的方程
-x+
=0有两个不相等的实数根，那样m最大整数值是（ ）
A.2; B.1; C.0; D.-1.
5.下列命题中,其逆命题是真命题的命题个数（ )
全等三角形的对应角相等; 对顶角相等; 等角对等边.
两直线平行,同位角相等; 全等三角形的面积相等;
1个; 2个; 3个; 4个.
6. 如图在ABC中,BC=8 AB的中垂线交BC于D, AC的中垂线交BC于E,则ADE的周长等于
A.8 B.4 C.12 D.16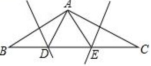 
2、填空题
7.当x____________________时，
无意义.
8.当____________________时，关于x的方程m-3x=
是一元二次方程。
9.方程=4x的解是__________ .
10.在实数范围内分解因式: 2
__________ .
11.已知平面直角坐标系中两点分别为A、B ,那样AB=__________.
12.已知直角三角形的两边长分别为5, 12 ,那样第三边的长为__________.
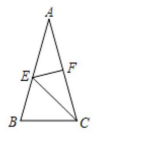
13.如图,在ABC中，AB= AC, 边AC的垂直平分线分别交边AB、AC于点E、F, 假如∠B=75°，那样
BCE=__________度.
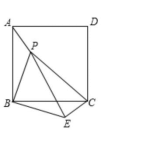
14.如图，p是正方形ABCD内一点,将ABP绕点B顺时针方向旋转能与CB重合,
若PB=3,则P =__________.
（13题图） （14题图） （15题图）
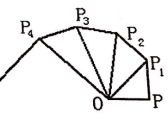
15.如图，OP=1 ,过点P作P
⊥OP ,且P=1 , 得O =2 ;再过点作
⊥O ,
且=1 ,得O
= ;又过点作
⊥O ,且=1 , 得O
=2 ;……这样办法作下去,那样0
= __________ .
16.以线段AB为腰且以A为顶角顶点的等腰三角形的第三个顶点C的轨迹是__________ .
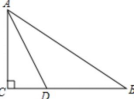
17.已知:如图,在ABC中，∠C=90°，AD平分CAB，BC=9cm，BD= 6cm,那样AB的长是__________.
18.如图，已知长方形ABCD中，AB=3，AD=5 ,把线段AD绕点A旋转,使点D落在直线BC.上的点F处,那样DF的长是__________.
（17题图） （18题图）
简答卷:
19.计算:
-
- 20.解方程: 
-3=28
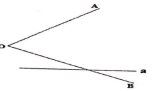
21.已知:∠AOB和直线a .求作:∠AOB内部一点P ,使点P到∠AOB的两边OA、OB与直线a的距离均相等.
22."引葭赴岸“是《九章算木》中的- -道題:”今有池一丈 ,葭生其中央,出水一尺，引葭赴岸,迺与岸芥.伺水深,葭氏各几何?"題意是:有一个边长为10尺的正方形池塘，一棵芦苇AB成长在它的中央,高出水面BC为1尺.假如把该芦苓沿与水池边垂直的方向拉向岸辺,那样芦革的顶部B恰好碰到岸边的B' . 向芦苇长多少?
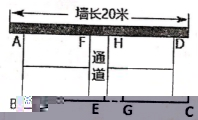
23.如图,用总长为80米的篱笆,在一面靠墙的空地上围成如图所示的花圃ABCD ,花圃中间有一条2米宽的人行通道,园艺师傅用篱笆围成了四个形状、大小一样的鲜花种植区
域,鲜花种植总面积为192平米,花圃的一边靠墙,墙长20米,求AB和BC的长.
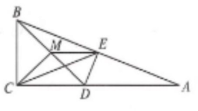
24.如图,在ABC中,ACB=90°,DE是AB边的垂直平分线,与AC交于点D,与AB交于点E，M是BD的中点
求证: CM= EM;
当线段AC长度改变时, CME与ABD的面积之比是不是发生变化?假如不变,求出比值;假如发生变化。说明怎么样变化.
4、综合能力题小题2分,第小题7分,第小题3分)
25.已知,点C是线段AB所在平面内任意一点,分别以AC、BC 为边,在AB同侧作等边ACE和等边△BCD ,联结AD、BE交于点P .
如图1 ,当点C在线段AB上移动时,线段AD与BE的数目关系是: __________。
如图2 ,当点C在直线AB外,且∠ACB <120度 ,仍分别以AC、BC为边,在AB同侧作等边MACE和等边△BCD ,联结AD、BE 交于点P . 的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时∠APE是否随∠ACB的大小发生变化?若变化,写出变化规律,若不变,请求出APE的度数。
如图3，在的条件下，求证：CP平分DPE。
