2017学年第二学期七宝中学高中二年级期末考试
数学考试试题
1、填空题
1.将三份录取公告书投入四个邮筒共有_______种不一样的投递方法。
2.若一个圆锥的侧面展开图是面积为2
的半圆面，则该圆锥的底面半径为____。
3.已知空间向量，如
果存在实数
使得
成立，则
_______.
4.在
展开式中，常数项为_______。（用数字作答）
5.从一堆苹果中任取6个，称得它们的水平如下（单位：克）：
125，124，121，123，127，则该样本标准差
=______克。
6，在上海高考考试改革策略中，需要每位高中生需要在物理、化学、生物、政治、历史、地理6门学科（3门理科，3门文科）中选择3门参加等级考试，小李同学受理想中的大学专业所限，决定至少选择一门理科学科，那样小李同学的选科策略有____种。
7.若在
展开式中，若奇数项的系数之和为32，则含
的系数是______。
8，已知实数
满足不等式组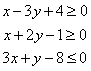
，若目的函数
恰好仅在点
处获得最大值，则实数
的取值范围为_______.
9.在
的展开式中，含
项的系数为______（用数字作答）
10．已知满足组合数方程
，则的最大值是_______.
11.设集合
，选择
的两个非空子集
和，要使中最小的数大于中最大的数，则不一样的选择办法共有______种。
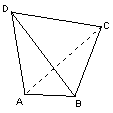
12．如图，
与
是四面体
中互相垂直的棱， 
,为常数，则四面体的体积最大值是_______.
2、选择题
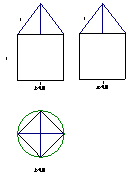13．一个空间几何体的三视图如图所示，则该几何体的体积为（ ）
A．
B．
C．
D．
14．从2018名学生志愿者中选取50名学生参加活动，若使用下面的办法选取，先用简单随机抽样从2018人中剔除18人，剩下的2000人再按系统抽样的办法抽取50人，则在2018人中，每个人入选的概率（ ）
A．不全相等 B.均不相等
C．都相等，且为 D.都相等，且为
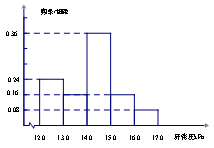15．为了研究某药厂的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据（单位：
）的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将它按从左到右的顺序分别编号为第一组、第二组、……，第五组，右图是依据实验数据制成的频率分布直方图，已知第一组与第二组共有20人，第三组中没疗效的有6人，则第三组中有疗效的人数为（ ）
A．6 B. 8 C.12 D.18
16.《算数书》竹简于上世纪八十年代在湖北江陵县张家山出土，这是国内现存最早的有系统的数学典籍，期中记载有求“盖”的术：置如其周，令相承也；又以高乘之。三十六成一。该术等于给出了圆锥的底面周长与高
,计算其体积,它事实上是将圆锥体积公式的圆周率近似取为3，那样近似公式等于将圆锥体积公式中的近似取为（ ）
A． B. C. D. 
3、解答卷
17.毕业季有6位好友欲合影留念，现排成一排，假如：
（1）
两人不排在一块，有几种排法？
（2）两人需要排在一块，有几种排法？
（3）不在排头，不在排尾，有几种排法？
18．已知在二项式
的展开式中，前三项系数的绝对值成等差数列。
（1）求正整数
的值；
（2）求展开式中二项式系数最大的项；
（3）求展开式中系数最大的项；
19．已知直线
（1）当
时，求
的交点坐标；
（2）过坐标原点
作的垂线，垂足为，为
的中点，当
变化时，求点的轨迹的参数方程，并指出它是什么曲线。
20.将4个不一样的红球和6个不一样的白球放入同一个袋中，现从中取出4个球。
（1）若取出的红球的个数不少于白球的个数，则有多少种不一样的取法；
（2）取出一个红球记2分，取出一个白球记1分，若取出4个球的总分不少于5分，择优多少种不一样的取法；
（3）若将取出的4个球放入一箱子中，记“从箱子中任意取出2个球，然后放回箱子中”为一次操作，假如操作三次，求恰有一次取到2个红球且有一次途径2个白球的概率。
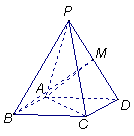
21.在四棱锥
中，底面是矩形，，
以
的中心为球心、为直径的球面交
于点，交于点。
（1）求证：
；
（2）求直线
所成角的大小；
（3）求点到平面
的距离。
